Reeks 1 : De Meta-Circulaire Evaluator

Deze oefeningenreeks behandelt de meta-circulaire evaluator uit hoofdstuk 4.1 van Structure and Interpretation of Computer Programs. Dit is een evaluator voor Scheme geschreven in Scheme. De oefeningen (en later ook de oplossingen) kan je vinden op de oefeningenwebsite.

De meta-circulaire evaluator start je door het bestand "icp_1_1_meval.scm" te evalueren in DrRacket. Er zijn dan tegelijkertijd 2 Scheme interpreters in het spel. Allereerst is er de Scheme evaluator van de omgeving waarin je aan het werken bent. Deze evaluator evalueert het programma dat je zonet gedownload hebt. Dit Scheme-programma is toevallig zelf een interpreter voor Scheme.

Wanneer je bij je experimenten met de meta-circulaire evaluator een foutmelding voorgeschoteld krijgt, kan je deze opnieuw starten door de parameterloze functie driver-loop op te roepen. De globale omgeving wordt dan niet geherinitialiseerd, waardoor je eventuele test-variabelen niet opnieuw moet toewijzen. Indien je de globale omgeving toch wil herinitialiseren, moet je de volledige evaluator opnieuw starten (ahv DrRacket’s run).

1 Soorten expressies

1.1 Oefening: Soorten expressies herkennen

De evaluator behandelt de verschillende soorten expressies elk op een specifieke manier. Welke soorten worden onderscheiden? In welke procedure vind je dit terug in de code? Hoe herkent deze procedure de verschillende expressies? Ga dit na voor volgende expressies.

(define x 4)

5

(* 3 4)

(set! x 99)

(lambda (a b) (* (+ a b) (- a b)))

1.2 Oefening: Expressies tracen

Ga na (trace de code en zie welke functies achtereenvolgens worden opgeroepen) hoe de evaluator de waarde (niet) berekent van de volgende expressies:

(+ 3 4)

(lambda () (+ 3 4))

+

'+

Opmerking: 'xxx en gelijkaardige expressies worden automatisch door de scheme-reader omgezet in "(quote xxx)". Een inverse transformatie gebeurt ook bij het afdrukken. Je zal als gebruiker dus nooit een lijstje van de vorm "(quote ...)" te zien krijgen, alhoewel quotaties intern wel zo voorgesteld worden.

2 Uitbreiden van de evaluator

Niet elke manier is echter geschikt voor elke uitbreiding. Afgeleide expressies kan je eenvoudig implementeren door deze te vertalen naar eenvoudigere expressies. Dit wil natuurlijk niet zeggen dat je het zo moet doen. Een expressie kan ook altijd rechtstreeks geëvalueerd worden door een specifieke evaluatie-functie. Dit is vaak zelfs efficiënter (maar wel moeilijker te implementeren).

2.1 Oefening: Extra primitieven

Test vervolgens of je uitbreiding werkt.

> (begin (display "azerty")(newline)          (display "qwerty"))

azerty qwerty ;;; M-eval value: #<void>

> (pair? (cons 1 2))

;;; M-eval value: #t

> (number->string 11 2)

;;; M-eval value: 1011

2.2 Oefening: and als special form

Voorzie de evaluator van een and. In welke van de categorieën valt een and-expressie?

Implementeer dit.

2.3 Oefening: and als afgeleide expressie

Implementeer nu deze manier.

> (and true true true)

;;; M-eval value: #t

> (and true false true)

;;; M-eval value: #f

> (and true true 'some-symbol)

;;; M-eval value: some-symbol

2.4 Oefening: or als afgeleide expressie

Pas de evaluator aan zodat de evaluator een or-expressie kan evalueren. Doe dit eerste als afgeleide expressie.

> (or false true true)

;;; M-eval value: #t

> (or)

;;; M-eval value: #f

> (or false false false)

;;; M-eval value: #f

> (or false 123 false)

;;; M-eval value: 123

2.5 Oefening: or als special form

Doe nu hetzelfde, maar met or als special form.

2.6 Oefening: let

Voorzie de evaluator van een let eens als special form en eens als afgeleide expressie van een expressie die de evaluator reeds kan interpreteren. Teken eerst de syntaxboom van deze expressie.

Hint: De expressie (let ((var-1 expr-1) ... (var-n expr-n)) body) is equivalent aan ((lambda (var-1 ... var-n) body) expr-1 ... expr-n)

(define (eval-let exp env)

...)

(define (let->applied-lambda exp)

...)

> (let ((a 1)         (b 2))     (cons a b))

;;; M-eval value: (1 . 2)

2.7 Oefening: let*

Voorzie de evaluator van een let*. Leg uit hoe een let* expressie kan herschreven worden als een reeks van geneste let expressies. Voorzie vervolgens de evaluator van een let* aan de hand van een transformatiefunctie: (define (let*->lets exp) ...)

Belangrijk: het resultaat van een oproep van deze functie is opnieuw een Scheme-expressie. Vergeet deze niet verder te evalueren.

> (let* ((a 3)          (b (cons 2 a)))     (cons 1 b))

;;; M-eval value: (1 2 . 3)

2.8 Oefening: let* als speciale vorm

Voorzie de evaluator van een let*. Maar implementeer let* nu als speciale vorm:

> (let* ((a 3)          (b (cons 2 a)))     (cons 1 b))

;;; M-eval value: (1 2 . 3)

2.9 Oefening: map

Schrijf zelf een hogere-orde my-map-functie en test deze uit in de meta-circulaire evaluator. Onderstaande interactie licht dit toe:

> (my-map (lambda (x) (cons x x)) '(1 2 3))

((1 . 1) (2 . 2) (3 . 3))

Beschouw map nu echter als een primitieve functie. De meta-circulaire evaluator moet applicaties van map dus evalueren door de map uit de onderliggende Scheme-omgeving op te roepen.

Wat gebeurt er als je deze map uittest? Verklaar.

2.10 Oefening: omgevingen

Ga na hoe de evaluator omgevingen beheert. Trace daarom doorheen de broncode van de evaluator wat er gebeurt wanneer volgende expressies uitgevoerd worden. Teken de omgevingsdiagrammen, procedure-objecten, etc. die onderweg aangemaakt worden.

Merk op: De expressies evalueren niet noodzakelijk naar een oplossing.

De oplossing bestaat uit een reeks diagrammen. Merk op dat we, hoewel we een diagram van de omgevingen aan het maken zijn, geen "omgevingsdiagram" zoals bij Structuur 1 meer aan het maken zijn. In plaats daarvan hebben we hier te maken met een hele boom cons-cellen. Om zeker te zijn dat er geen verwarring is beschrijf ik hier nog eens expliciet de notatie-conventies: een cons-cel wordt weergegeven door twee vierkantjes die tegen elkaar geplakt zijn. Één van beide vierkanten is de car, het andere vierkant is de cdr. In zowel de car als de cdr staat een bolletje van waaruit een pijl vertrekt. Die pijl wijst naar wat ’in’ de car of cdr ’zit’. Dit kan een cijfer zijn, een symbool, een ingebouwde (DrRacket-) procedure zoals "#<procedure:+>", een cons-cel of een lijst van symbolen en cijfers.

Weet dat zo’n gequote lijst eigenlijk gewoon meer cons-cellen zijn; ik schrijf ze enkel verkort op als het mij lijkt dat het jullie alleen maar méér gaat verwarren om nog meer cons-cellen te tekenen. Cruciaal is echter dat in Scheme zo’n pijl niet kan wijzen naar een car of een cdr van een cons-cel: als de pijl naar een cons-cel wijst, wijst die altijd naar de gehele cons-cel, zelfs als de pijl in het diagram toekomt in de car of de cdr.

Sommige cons-cellen in de diagrammen hebben een kleur. Die kleur betekent natuurlijk niets voor Scheme; en wordt enkel gebruikt om het diagram voor jullie overzichtelijker te maken. Deze legende verklaart hoe de kleuren gebruikt worden:

De kleuren hebben natuurlijk geen invloed op de betekenis of op het gedrag. Om het verschil tussen de "omgevingen" en "frames" enerzijds, en het verschil tussen de verschillende omgevingen anderzijds, zo duidelijk mogelijk te maken, worden alle cellen die bij één omgeving horen, omvat door een lichtblauwe kader. Alle cellen die bij één frame horen, worden omgeven door een lichtrode kader.

Initieel, voordat de eerste expressie hieronder uitgevoerd wordt, ziet de globale omgeving er dus zo uit:

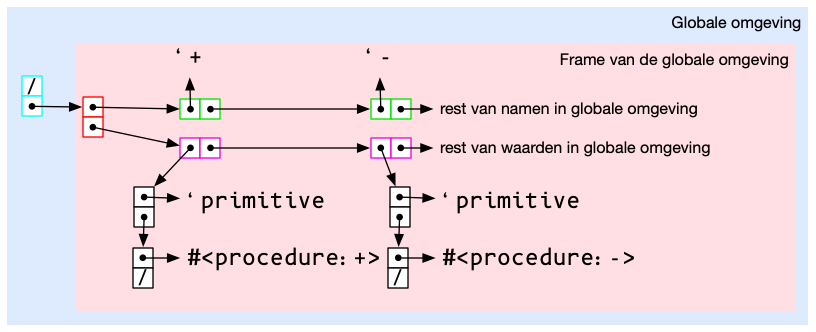
1. (define x 4)

2. (set! x 4)

3. ((lambda (x)

   (define (f a b)

   (+ a b b))

   (define (g x)

   (let ((y (+ x 1)))

   (f x y)))

   (g x))

   123)

4. (let ((a 1)

   (b (* a 2)))

   b)

5. (let* ((a 1)

   (b (* a 2)))

   b)

6. (define (f n)

   (define (g m)

   (f (+ m 1)))

   (g n))

   (f 1)

7. (define (h)

   (define (i n)

   (j n))

   (define (j m)

   (i (+ m 1)))

   (i 2))

   (h)

2.11 Oefening: tab (examenoefening)

Breid de meta-circulaire evaluator uit met ondersteuning voor zogenaamde tab expressies. De syntax van deze expressies is als volgt: (tab <size-exp> <filler-exp>)

Zulk een tab expressie evalueert naar een nieuwe vector. Hiertoe neemt zij als eerste argument een expressie die eenmaal geëvalueerd wordt om de grootte van de aan te maken vector te bekomen. Om de elementen van de vector op te vullen, neemt zij als tweede argument een expressie. Deze expressie wordt meermaals geëvalueerd; één evaluatie per element van de vector (van links naar rechts). Volgend transcript licht het gebruik van tab verder toe:

> (define x 5)

;;; M-eval value: ok

> (tab 3 (begin (set! x (+ x 1)) x))

;;; M-eval value: #(6 7 8)

> x

;;; M-eval value: 8

Breid nu de meta-circulaire evaluator uit met ondersteuning voor zogenaamde inc (“increment”) expressies. De syntax van deze expressies is als volgt: (inc <var-name>).

Zulk een inc expressie neemt als enige argument een aan een getal gebonden variabele, verhoogt hiervan destructief de waarde met 1, en geeft de nieuwe waarde van de variabele terug.

Volgend transcript volgt op het vorige en licht het gebruik van inc verder toe:

> (inc x)

;;; M-eval value: 9

> (tab 4 (inc x))

;;; M-eval value: #(10 11 12 13)

Implementeer inc als een afgeleide expressie a.d.h.v een procedure inc->begin.

2.12 Oefening: freeze (examenoefening)

Voeg aan de meta-circulaire evaluator van Scheme de special form freeze toe a.d.h.v. een predikaat freeze? en een procedure eval-freeze?. Als je deze operatie toepast op een variabele, wordt het onmogelijk om die variabele destructief aan te passen. Bijvoorbeeld, na een (freeze a) op een bestaande variabele a krijg je een foutmelding bij (set! a 42).

Let op dat de scoping regels gerespecteerd blijven; het volgende voorbeeld mag geen fout melden.

> (define a 2)

;;; M-eval value: ok

> (define b 3)

;;; M-eval value: ok

> (define c 4)

;;; M-eval value: ok

> (freeze a)

;;; M-eval value: done

> (freeze c)

;;; M-eval value: done

> (define (set-fn! x y)      (define a 0)      (set! a x)      (set! b y)      (list a b c))

;;; M-eval value: ok

> (set-fn! 0 1)

;;; M-eval value: (0 1 4)

Maar als je hier nog het volgende aan toevoegt, moet je een foutmelding krijgen voor de toekenning aan b:

> (begin      (freeze b)      (set-fn! 5 6))

Trying to assign a frozen variable -- SET! 'b

Opmerking: Behalve het toevoegen van een freeze special form zal je in deze oefening wijzigingen moeten aanbrengen aan de manier waarop variabelen bijgehouden worden in de omgevingen, zodat je variabelen als “bevrozen” kan markeren. Ook zal je de code die waarden toekent aan variabelen moeten aanpassen om die “bevrozen” toestand te detecteren, en in dat geval een foutboodschap te geven.

2.13 Oefening: while en until

Voeg aan de evaluator de controlestructuren while en until toe door de functies eval-while en eval-until te implementeren.

Je kan de volgende syntax voor de controlestructuren gebruiken: (while condition body ...) (until condition body ...)

> (define i true)

;;; M-eval value: ok

> (while i          (display "in while: ")(display i)(newline)          (set! i false))

in while: #t ;;; M-eval value: #<void>

> (until i          (display "in until: ")(display i)(newline)          (set! i true))

in until: #f ;;; M-eval value: #<void>

2.14 Extra oefening voor thuis: bitwise-and

Voeg de functie bitwise-and toe aan de evaluator als nieuwe primitieve. Deze functie neemt twee getallen en neemt de binaire AND ervan.

> (bitwise-and 2 3)

2

2.15 Extra oefening voor thuis: shift

Een veel voorkomende operatie op binaire getallen zijn zogenaamde shifts. Hierbij wordt de binaire representatie van het getal enkele malen naar links of rechts geschoven.

Implementeer deze shift als primitieve procedure.

> (shift 1 2)

4

> (shift 3 1)

6

> (shift 4 -1)

2

3 De analyzing evaluator

Deze laatste oefeningen behandelen de analyzing meta-circulaire evaluator uit hoofdstuk 4.1.7 van Structure and Interpretation of Computer Programs. Dit is een alternatief op de meta-circulaire evaluator die de analyse van de syntax ontkoppelt van de uitvoering van het programma. Deze evaluator start je door het bestand "icp_2_aeval.scm" te evalueren in DrRacket.

3.1 Verschil in uitvoertijd ten gevolge van analyse

3.2 Stapels van evaluatoren

Wanneer we de analyzing evaluator uitvoeren bovenop de DrRacket evaluator, kan tijd bespaard worden wanneer expressies herhaaldelijk uitgevoerd worden. Net als de ’gewone’ meta-circulaire evaluator, is de analyzing evaluator echter meta-circulair. Dit houdt in dat het mogelijk moet zijn om de analyzing evaluator uit te voeren binnen een analyzing evaluator die op zijn beurt binnen bv. de DrRacket evaluator uitvoert (of, natuurlijk, opnieuw binnen een analyzing evaluator. Of binnen een meval).

Beredeneer of het uitvoeren van een meta-circulaire evaluator binnen een analyzing evaluator (a.a) sneller kan zijn dan het uitvoeren van diezelfde meta-circulaire evaluator binnen een niet-analyzing evaluator (a.b).

Beredeneer of het uitvoeren van een analyzing evaluator binnen een meta-circulaire evaluator (dus niet bv. rechtstreeks binnen DrRacket, b.a) sneller kan zijn dan het uitvoeren van een niet-analyzing evaluator binnen diezelfde meta-circulaire evaluator (b.b).

Beredeneer vervolgens of de situatie in c.a sneller kan zijn dan die in c.b, en of deze sneller kan zijn dan deze in c.c.

3.3 Fractie van uitvoertijd gespendeerd aan analyse

Gebruik bv. de time procedure ((#%require (only racket/base time))) om na te gaan hoeveel tijd er gespendeerd wordt aan de syntactische analyze, t.o.v. aan de uitvoering van expressies.