Higher-Order Programming » Lab Sessions

Session 0

Lecturer: Jens Nicolay (jens.nicolay@vub.be) Assistant: Bjarno Oeyen (bjarno.oeyen@vub.be)

Installing and Configuring DrRacket

Please read this guide on how to install, and configure, DrRacket for this course. Return to this page after you have executed the hello world example.

A Quick Start to DrRacket

Welcome to the wonderous world of programming in the Scheme programming language. Come one, come all! Take a seat and let's get going...

The following is an overview of the DrRacket IDE.

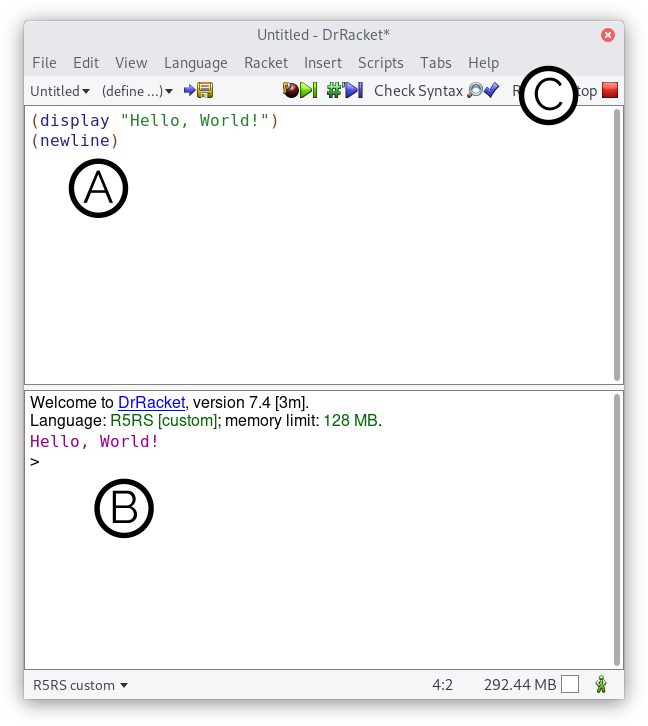
(A) shows the definitions panel. In this panel, you can type code to be evaluated by the Scheme interpreter bundled with DrRacket.

(B) shows the interactions panel. In this panel, you have access to a running Scheme evaluator via the Read-Eval-Print Loop (REPL). Use this panel to quickly type a Scheme expression and to immediately evaluate it.

(C) shows the menu bar. There are various buttons here, but the most frequenly used buttons are the «Run» (CTRL/⌘+R) and «Stop» (CTRL/⌘+B) buttons.

If you want to keep your code, write it in the definitions panel. If you click on the «Run» again, the interactions panel is cleared with a new Scheme REPL. Therefore, in these exercises write all code in the definitions panel such that you can save your solutions to refer to later.

Numbers, Strings, Booleans...

The Scheme programming has access to numerous data types. In the first exercises we will be focussing on primitive data types such as numbers, strings, and booleans.

Scheme is a dynamically-typed programming language. In short, this means that values have types, but variables do not.

---

Exercise 1: For the following values, what types of values do they resemble? What happens when you type each of these values in the REPL?

123 -42 0.33333 1/3 #t #f "hello" "" "world" modulo even? + >= string-length

Combinations

In the previous section we have experimented with some primitive values in Scheme, but using primitive values alone we cannot build any large complex programs. Let's keep experimenting in the REPL for a short while.

Combinations combine other primitive, and compound, expression in a sequence wrapped between ( and ). In this example, we have made 3 examples of combinations that can be evaluated by a Scheme evaluator. Combinations often result in procedure applications, but this is not always the case (an example will follow in a later exercise).

---

Exercise 2: Predict the outcome of the following expressions. Verify using the Read-Eval-Print Loop.

(string-length "VUB") (abs -7) (modulo 13 4) (even? 19) (string-length (string-append "Hello " "World")) (string? "Guy L. Steele") (number? "Gerald Jay Sussman") (procedure? modulo) (procedure? procedure?) (boolean? (string? 5)) (+ 10 15) (- 5) (/ 6 2) (+) (- 100 (* 5 5)) (/ (+ 100 200 300) 3)

Exercise 3: Convert the following into an equivalent Scheme expression. Note that Scheme uses prefix notation!

$$e_1 = \frac{a + b}{2}$$

$$e_2 = \frac{a + b}{e} - \frac{c + d}{f}$$

$$e_3 = a\times{}a + 2\times{}a\times{}b + b\times{}b$$

$$e_4 = \frac{a + \frac{b}{c}}{d} \times \frac{e}{\frac{g}{i} - h}$$

Make use of define to add a variable to the environment. E.g.

(define pi 3.14159265) (* 2 pi 4) ; -> 25.1327412 (circumference of a circle with radius 4)

The ; (semicolon) character is used in Scheme to denote end-of-line comments.

Procedures

Up until now we have only used the primitive procedures that are available in Scheme, let's make a procedure ourselves! In Scheme, new procedures are created using lambda. The following is a procedure that increments a given number by one.

(lambda (a) (+ a 1)) ; -> #<procedure>

If we want to use the procedure, we create a combination where the procedure is the first item in the combination. For example:

((lambda (a) (+ a 1)) 10) ; -> 11

However, if we want to use a procedure multiple times, it is a good idea to define it...

(define add1 (lambda (a) (+ a 1))) (add1 10) ; -> 11

There is a short-hand notation for define that immediately creates (and defines) a procedure object, we can thus, rewrite this program as follows...

(define (add1 a) (+ a 1)) (add1 10) ; -> 11

---

Exercise 4: Define a procedure called double that multiplies a number by two.

Exercise 5: Define a procedure called square that multiplies a number by itself.

Exercise 6: Define a procedure called celsius-to-fahrenheit that converts a temperature from degrees Celsius to degrees Fahrenheit. You can use the following formula...

$$F = (C + 40) \times 1.8 - 40$$

As an optional exercise, invert the formula and implement fahrenheit-to-celsius.

Exercise 7: Define a procedure called average-of-three that has 3 parameters and calculates the average value of 3 numbers.

Special Forms

Not every expression of the form (foo ...) results in a procedure application. For some keywords, the Scheme evaluator will not execute a procedure application, but will perform another kind of application.

---

Exercise 8: In the section about procedures, can you identify which combinations are not procedure applications. Explain how you arrived at this conclusion?