Higher-Order Programming » Lab Sessions

Session 8

Assistant: Steven Keuchel (steven.keuchel@vub.be)

Section 1: Understanding The Metacircular Scheme evaluator

Download the metacircular implementation and open this file in DrRacket. In contrast to previous exercises that required you to make use of a file, you will need to make direct changes to this file. So be sure to keep a copy of the original file in case you wish to revert your changes.

In the implementation of the metacircular evaluator we redefine apply, which is not allowed by default in the R5RS implementation bundled with Racket. You may have to configure DrRacket to allow this redefinition. See the instructions from the first lab session. Be sure to uncheck "Disallow redefinition of initial bindings"!

The foundations

The metacircular implementation can be difficult to understand, since multiple components are inherently dependent on each other. The figure below showcases the four important components.

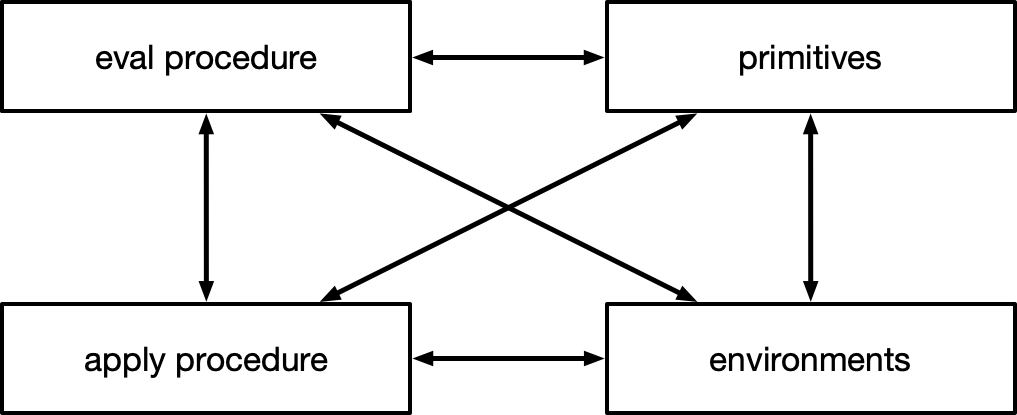
The eval procedure

(define (eval exp env) (cond ((self-evaluating? exp) exp) ((variable? exp) (lookup-variable-value exp env)) ((quoted? exp) (text-of-quotation exp)) ((assignment? exp) (eval-assignment exp env)) ((definition? exp) (eval-definition exp env)) ((if? exp) (eval-if exp env)) ((lambda? exp) (make-procedure (lambda-parameters exp) (lambda-body exp) env)) ((begin? exp) (eval-sequence (begin-actions exp) env)) ((cond? exp) (eval (cond->if exp) env)) ((application? exp) (apply (eval (operator exp) env) (list-of-values (operands exp) env))) (else (error "Unknown expression type -- EVAL" exp))))

This procedure dispatches over the different types of expressions. After an expression has been entered in the REPL, it will be sent to this procedure for further evaluation. There are multiple branches here, and every branch represents one type of expression.

If you want to add new special forms (syntax), you have to add them to this condtional.

The apply procedure

(define (apply procedure arguments) (cond ((primitive-procedure? procedure) (apply-primitive-procedure procedure arguments)) ((compound-procedure? procedure) (eval-sequence (procedure-body procedure) (extend-environment (procedure-parameters procedure) arguments (procedure-environment procedure)))) (else (error "Unknown procedure type -- APPLY" procedure))))

This procedure is executed when the expression in eval is an application (it is a list). eval already evaluated both the operator expression and the argument expressions, therefore apply receives the procedure object (or something that is not a procedure: and therefore should raise an error) and a list of argument values.

Ignoring the error case, there are two options. Either a primitive procedure needs to be applied (a procedure that is given by the language implementation itself), or a user-defined (compound) procedure that is implemented by the user of the metacircular evaluator.

In the latter case, the body of the procedure is evaluated in the lexical scope that is created by extending the environment of the procedure object with the bindings that bind the formal parameters to the actual values.

The duality of eval and apply

The two most important componenets of the metacircular evaluator are eval and apply. We also need primitives and environments as part of a working language, but the heart of the implementation can be found in only eval and apply. The difference between eval and apply is...

• eval takes an expression and an environment as input, and calls apply (when appropriate) with a procedure value, and a list of arguments.
• apply takes a procedure and arguments, and calls eval with an expression (the body of the procedure), and an environment (the extended environment)

Primitives

Primitive procedures are the foundation blocks on which new programs can be build. A Scheme evaluator by default comes with many primitives. For simplicity, only the most important ones are supplied in our metacircular implementation.

(define primitive-procedures (list (list 'car car) (list 'cdr cdr) (list 'cons cons) (list 'null? null?) (list 'list list) (list '+ +) (list '- -) (list '* *) (list '/ /) (list '= =) (list 'newline newline) (list 'display display)))

The variable primitive-procedures contains a list of all built in procedures. Each element of this list is a list of size 2, where the first element is the name (as a symbol) of the procedure: this is how it will be available in the global environment. The second element is the procedure object itself. In this metacircular Scheme evaluator the built-in procedure itself is made available.

Next to primitive operations there are special forms. Remember that the eval procedure dispatched over the different types of expressions. The main difference between procedures and special forms in the metacircular evaluator is that special forms work on expressions, and procedures work on evaluated expressions (i.e., values).

During the exercises we will delve in both procedures and special forms.

Environments

The last important component of the metacircular Scheme evaluator are environments. An environment can be seen as pair containing a frame, and a base environment. A frame is the combination of two lists: a list of variable names and a list of values that represents the bindings.

(define (enclosing-environment env) (cdr env)) (define (first-frame env) (car env)) (define the-empty-environment '()) (define (extend-environment vars vals base-env) (if (= (length vars) (length vals)) (cons (make-frame vars vals) base-env) (if (< (length vars) (length vals)) (error "Too many arguments supplied" vars vals) (error "Too few arguments supplied" vars vals)))) (define (make-frame variables values) (cons variables values)) (define (frame-variables frame) (car frame)) (define (frame-values frame) (cdr frame))

Every environment has an enclosing environment, except for the global environment which is the empty environment. Check the implementation of lookup-variable-value, set-variable-value!, and define-variable! for how special forms like define and set! operate, and how variables are resolved to their values.

Section 2: Primitive Procedures

In these exercises we are going to work on the metacircular implementation of Scheme in the Scheme implementation Racket. Remember that an evaluator is just a procedure (i.e. lambda) that when applied to an expression, performs the required actions to evaluate that expression. In other words, an evaluator is just another program. If we implement an evaluator in the same programming language for which we write an eval- uator, we call this a metacircular evaluator. Since a Scheme expression is actually just a list, a Scheme evaluator is nothing more than a list processing program.

Exercise 1: Division by Zero

Currently, the / procedure in the metacircular evaluator will make use of the / procedure from the host environment. Since that procedure raises an error when the divisor is equal to the number zero, the metacircular evaluator will stop working due to this error.

Instead of catching errors from the host environment in the metacircular evaluator, you will modify the / procedure in the metacircular evaluator such that it returns the number zero instead[^divisionbyzero]. Therefore, you get the following behaviour in your modified metacircular evaluator.

[^divisionbyzero]: This is not entirely correct as it should return NaN (not a number). However, this value is not available in Scheme. Therefore, if you want to be correct, you can also choose to return 'nan (as a symbol) instead, or +inf.0 or -inf.0 to represent an infinite value (depending on the sign of the dividend).

(define a 12) (define b 6) (/ (+ a b) (- a (* b 2))) ; -> 0

Section 2: Syntactic Sugar

Exercise 2: Implementing when

Before delving in how special forms can be implemented we will explore how new syntactic constructs can be created by using syntactic sugar: by expanding a Scheme expression from one form, into another.

Currently, when you want to execute multiple expressions when a condition is true, you have to wrap all expressions in a begin, even when there is no "alternative" branch.

(if (something-true? x) (begin (display "it's true!") (do-calculation x)))

Wouldn't it be better if this program could be written as follows.

(when (something-true? x) (display "it's true!") (do-calculation x)))

Hint! Just as before, it can help to create accessor procedures that make it easier to retrieve values stored in the when expression: the condition, and the expression sequence stored within. Remember that code is data!

Expand (eval exp env) with a case that when it encounters a when, it will transform this expression to the corresponding program using only if and begin, and then apply eval on this transformed program.

Hint! Check how cond is supported in the current implementation for an example.

Hint! If you wish to check a part of your implementation, without starting the metacircular REPL you can uncomment (driver-loop) at the bottom of the file!

Exercise 3: Implementing let

Do the same thing for adding support for the let syntax: remember that for each well-formed let expression, an equivalent expression using lambda can be written (refer to earlier exercises that used this property). Make use of the same technique as in the previous exercise.

Hint! Just as before, it can help to create accessor procedures that make it easier to retrieve values stored in the let expression.

1. Create the accessor procedures: (let-body, let-clauses, let-clause-name, let-clause-expression).
2. Create a lambda expression where the formal parameters are the let-clause-names of the clauses, and the body is the let-body
3. Create an application expression where the procedure is the one created in the previous step, and the arguments are the let-clause-expressions of the clauses.

Section 3: Special Forms

After adding new syntactical constructs to our Scheme evaluator by transforming one expression into another, we will look at how they can be implemented directly without transforming their program text to an equivalent program text using lower constructs (such as lambda, instead of let).

Exercise 4: Implementing when

Repeat exercise 3, this time by implementing the behaviour of when manually.

It should...

• First evaluate the boolean expression
• After it has been evaluated, its value should be checked.
  • If it is true: evaluate the expression sequence
  • Otherwise: do nothing

Hint! Start by looking at the evaluation of if, and adapt. The value returned by when when the conditional expression returned false is unspecified.

Exercise 5: Implementing let

Repeat the same for adding support for let.

It should...

• Evaluate for every clause the expression stored
• Create a new environment containing the bindings necessary in the let
• Evaluate the expression sequence in the extended environment.
• Return the result of evaluating the expression sequence

Hint! You can reuse the syntactical accessors from exercise 4.