Research Topics in Software Quality – Session 1: Lime Concolic Tester

In this exercise session, we will use the Lime Concolic Tester (LCT), a dynamic symbolic execution tool that can automatically find defects in Java programs and that can be helpful to generate test cases.

Course Homepage: http://soft.vub.ac.be/~cderoove/software_quality/

LCT Homepage: http://www.tcs.hut.fi/Software/lime

1 Basic Concepts

Consider the following program fragment. 

x = input();
x = x + 5;

if (x > 0)
    y = input();
else
    y = 10;

if (x > 2)
    if (y == 2789)
        throw new Exception("Error")

This program is composed of a sequence of statements, and can be visualized as a control flow graph, made up of nodes representing statements, connected with edges. Edges can be labelled with conditionals. Figure 1 represents the control flow graph of the previous program. Branch nodes are represented with diamonds in the graph. We can see that this program contains six branches (two for each if statement, one branch for the then part, one for the else part). How many paths can it take?

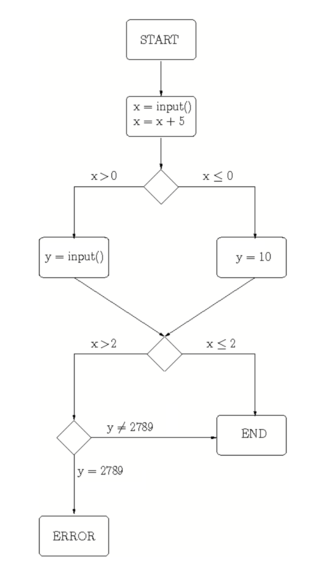
cfg.png

Figure 1: Control Flow Graph Example

2 Branch coverage and path coverage

public static void testme(int x, int y) {
    if (x > y) {
        if (x % 2 != 0) {
            x--;
        }
        if (x + y > 0) {
            y = 1;
        } else {
            y = 2;
        }
    }
}
  1. Draw the CFG of the testme function.
  2. How many branches and paths are there in the testme function? (All paths are feasible.)

  3. Write test cases for the testme function to cover:

    1. All branches
    2. All paths

    Is it easier to write a test suite with 100% branch coverage or with 100% path coverage? Why?

Consider the following program and test cases. 

public static void testme2(int x, int y) {
    if (x > 0) {
        y = 0;
    }
    if (y > 0) {
        x = 0;
    }
    y = x / (y + 1);
}

public static void test() {
    testme2(1, 1);
    testme2(0, 1);
}
  1. What is the branch coverage and path coverage of this set of test cases?
  2. Can you find an input generating an error for this program?

3 Symbolic execution

Before looking at concolic testing, let's take a quick look at how to execute a program symbolically. Consider again the following program. 

 1: x = input();
 2: x = x + 5;
 3: 
 4: if (x > 0)
 5:     y = input();
 6: else
 7:     y = 10;
 8: 
 9: if (x > 2)
10:     if (y == 2789)
11:         throw new Exception("Error")

A concrete execution (that is, normal execution) of this program will read its input values from the user and execute normally.

If this program is executed symbolically:

  1. On line 1, x will be bound to a symbolic variable, say a
  2. On line 2, the value of x is updated and becomes the symbolic value a + 5
  3. On line 4, since x is not bound to a concrete value, we cannot know whether the true or false branch will be taken. Both have to be explored, and we store constraints induced by the condition for each branch. This will lead to two possible execution states:
    1. x > 0, and y is bound to a new symbolic variable, say b
    2. x <= 0, and y is bound to 10
  4. …

This process generates a symbolic execution tree, annotated with constraints on the symbolic variables. The final tree is depicted on Figure 2, with edges annotated in red with constraints, and in blue with updates to the symbolic environment, that maps program variables to symbolic values.

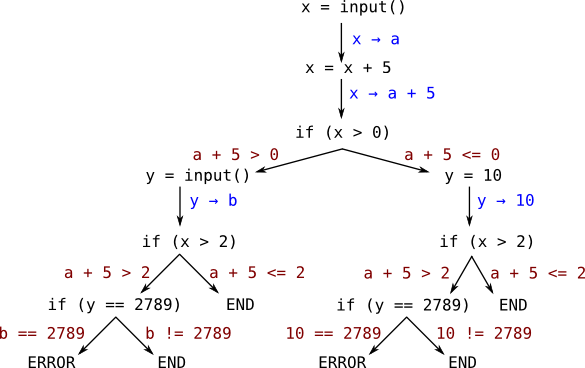
symextree.png

Figure 2: Symbolic Execution Tree Example

We can see from this tree that the program has 6 possible paths. Each path is associated with a path constraint, which is a constraint on the symbolic values that tells us with which values the program will follow this path. This path constraint is formed by taking the conjunction of the local constraint produced along the path. For example, the path constraint of the leftmost path reaching the error state is:

\begin{gather*} a + 5 > 0 \wedge a + 5 > 2 \wedge b = 2789 \\ \Leftrightarrow \\ a > -3 \wedge b = 2789 \end{gather*}

By solving this path constraint, we can find values leading to this error (e.g., a = 0, b = 2789). Path constraints that are not solvable correspond to infeasible paths (e.g., the rightmost error state, because y is bound to 10 and can therefore never be equal to 2789).

4 Concolic testing

Concolic testing combines concrete execution with symbolic execution. The analyzed program is first instrumented in order to add code that deals with the symbolic part of the analysis. It is then being run with random input values, and the concrete execution will explore one possible path, while the code added during instrumentation will generate the corresponding part of the symbolic tree, with the path constraint. Once the program terminates, a component of the path constraint can be negated in order to find values that explore a different path from the one taken. By repeating this multiple times, a large portion of the symbolic tree can be explored.

Take the same program as example. 

x = input();
x = x + 5;

if (x > 0)
    y = input();
else
    y = 10;

if (x > 2)
    if (y == 2789)
        throw new Exception("Error")

The first run is made with random values, say a = 0, b = 0. The concrete run explores the path corresponding to the following path constraint.

\begin{gather*} a + 5 > 0 \wedge a + 5 > 2 \wedge b \neq 2789 \\ \Leftrightarrow a > -3 \wedge b \neq 2789 \end{gather*}

The concolic testing engine then negates a conjunct of this path constraint, giving for example (reversing the last conjunct): \[ a > -3 \wedge b = 2789 \]

Passing this formula through an SMT solver allows the concolic testing engine to find new inputs, say a = 0, b = 2789. This will explore the error state. The first conjunct can then be negated to explore the other part of the symbolic execution tree.

Let's take the following function: 

public static void testme3(int x, int y) {
    if (x > y) {
        if (x % 2 != 0) {
            x--;
        }
        if (y % 2 != 0) {
            y--;
        }
        if (x + y > 0) {
            if (x * y > 0) {
                y = 1;
            } else {
                y = 2;
            }
        } else {
            y = 3;
        }
    }
}
  1. Draw the symbolic execution tree of this function
  2. List the path constraints that will be generated if this function is executed symbolically (treat the arguments as symbolic input)
  3. Perform concolic testing by hand on this function.

5 LCT Installation

Install LCT following the instructions here.

6 The Lime Concolic Testing Engine

LCT allows you to perform concolic testing by specifying which input should be symbolic. LCT automatically performs the instrumentation, the exploration of the symbolic execution tree, the solving of the constraints, and will list as output a number of generated input to explore a large part of the symbolic execution tree.

To verify a Java program with LCT, you need to adapt it to use symbolic values. First of all, you should import fi.hut.ics.lime.tester.LCT. You can then use the following functions to get symbolic input, defined in source/tester/src/main/java/fi/hut/ics/lime/tester/LCT.java:

  • int getInteger()
  • int getInteger(int min, int max)
  • boolean getBoolean()
  • byte getByte()
  • char getChar()
  • short getShort()
  • long getLong()
  • Object getObject(String name)

For example: 

import fi.hut.ics.lime.tester.LCT;

public class Foo
{
    public static void main(String[] args) {
        int x = LCT.getInteger();
        System.out.println(x);
    }
}

7 Simple example

public class FirstExample
{
    public static void testme(int x, int y) {
        System.out.println("x = " + x + ", y = " + y);
        if (x > y)
            if (x * y == 1452)
                if (x >> 1 == 5)
                    y = y / (x - 10);
    }

    public static void main(String[] args) {
        if (args.length < 2) {
            System.out.println("Please provide two integers as arguments");
            System.exit(1);
        }
        testme(Integer.parseInt(args[0]), Integer.parseInt(args[1]));
    }
}
  1. What is erroneous in this program?
  2. Can you find values of x and y to make this program crash?
  3. Draw the CFG of the testme function. How many branches does this function have? How many possible paths can be taken by this function?
  4. Draw the symbolic execution tree of the testme function, assuming x and y are symbolic input. Deduce the path constraints.
  5. Adapt the FirstExample program to use symbolic input values.
  6. Run LCT on the program (see Installing and running LCT). Does it find a potential error? Can you justify it?

8 Elevator example

Adapt the following program to use symbolic input, and run it with LCT. 

public class Elevator
{
    static int currentFloor;

    public static void main(String args[])
    {
        currentFloor = 1;
        int targetFloor = 5;

        int start = 1;
        int end = 10;

        if (currentFloor == 1 && targetFloor == 1)
            targetFloor = 1/0; // error

        if (currentFloor >= start && currentFloor <= end &&
            targetFloor >= start && targetFloor <= end) {
            move(targetFloor);

            if (targetFloor != currentFloor)
                targetFloor = 1/0;
        }
    }

    public static void move (int floor)
    {
        int moves = floor - currentFloor;

        if (moves < 0)
            moves = moves * -1;

        while (moves > 0) {
            if (currentFloor > floor)
                currentFloor = down(currentFloor);
            else
                currentFloor = up(currentFloor);

            moves = moves - 1;
        }
    }

    public static int down (int floor)
    {
        floor = floor - 1;
        return floor;
    }

    public static int up (int floor)
    {
        floor = floor + 1;
        return floor;
    }
}

9 Objects example

Consider the program below. This example already uses symbolic input.

  1. Draw the symbolic execution tree of this program and compute the path conditions. How many different paths exist in this program?
  2. Are all the branches covered by LCT?
import fi.hut.ics.lime.tester.LCT;

public class ObjPaths
{
    public int v;

    public static void main(String args[])
    {
        ObjPaths l1 = (ObjPaths)LCT.getObject("ObjPaths");
        ObjPaths l2 = (ObjPaths)LCT.getObject("ObjPaths");
        int y       = LCT.getInteger();

        if (l1 != null && l2 != null)
            if (l1.v == l2.v) {
                if (y == 100)
                    System.out.println("y = 100");
                else
                    System.out.println("y != 100");

                if (l1 == l2)
                    System.out.println("Foo");
                else
                    System.out.println("Bar");

            }

        System.out.println("END");
    }
}

10 Sort example

Adapt the following program to use symbolic values instead of random ones, and run it with LCT. Did LCT find an error? If not, what prevents you to conclude that the program is correct? 

import java.util.Random;

public final class Sort {
    static class IntContainer implements Comparable {
        public int value;

        public IntContainer()
        {
        }

        public IntContainer(int v)
        {
            value = v;
        }

        public int compareTo(Object o) {
            IntContainer i = (IntContainer)o;

            if (this.value > i.value)
                return 1;
            else if (this.value == i.value)
                return 0;
            else
                return -1;
        }
    }

    /**
     * Quicksort algorithm.
     * @param a an array of IntContainer items.
     */
    public static void quicksort(IntContainer[] a)
    {
        quicksort(a, 0, a.length-1);
    }

    private static final int CUTOFF = 10;

    /**
     * Method to swap to elements in an array.
     * @param a an array of objects.
     * @param index1 the index of the first object.
     * @param index2 the index of the second object.
     */
    public static final void swapReferences(Object[] a, int index1, int index2)
    {
        Object tmp = a[index1];
        a[index1] = a[index2];
        a[index2] = tmp;
    }

    /**
     * Return median of left, center, and right.
     * Order these and hide the pivot.
     */
    private static IntContainer median3(IntContainer[] a, int left, int right)
    {
        int center = (left + right) / 2;
        if(a[center].compareTo(a[left]) < 0)
            swapReferences(a, left, center);
        if(a[right].compareTo(a[left]) < 0)
            swapReferences(a, left, right);
        if(a[right].compareTo(a[center]) < 0)
            swapReferences(a, center, right);

            // Place pivot at position right - 1
        swapReferences(a, center, right - 1);
        return a[right - 1];
    }

    /**
     * Internal quicksort method that makes recursive calls.
     * Uses median-of-three partitioning and a cutoff of 10.
     * @param a an array of IntContainer items.
     * @param left the left-most index of the subarray.
     * @param right the right-most index of the subarray.
     */
    private static void quicksort(IntContainer[] a, int left, int right)
    {
        if(left + CUTOFF <= right)
        {
            IntContainer pivot = median3(a, left, right);

            // Begin partitioning
            int i = left, j = right - 1;
            for( ; ; )
            {
                while( a[++i].compareTo(pivot) < 0) { }
                while( a[--j].compareTo(pivot) > 0) { }
                if(i < j)
                    swapReferences(a, i, j);
                else
                    break;
            }

            swapReferences(a, i, right - 1);   // Restore pivot

            quicksort(a, left, i - 1);    // Sort2 small elements
            quicksort(a, i + 1, right);   // Sort2 large elements
        }
        else  // Do an insertion sort on the subarray
            insertionSort2(a, left, right);
    }

    /**
     * Internal insertion sort routine for subarrays
     * that is used by quicksort.
     * @param a an array of IntContainer items.
     * @param left the left-most index of the subarray.
     * @param right the right-most index of the subarray.
     */
    private static void insertionSort2(IntContainer[] a, int left, int right)
    {

        for(int p = left + 1; p <= right; p++)
        {
            IntContainer tmp = a[p];
            int j;

            for(j = p; j > left && tmp.compareTo(a[j - 1]) < 0; j--)
                a[j] = a[j - 1];
            a[j] = tmp;
        }
    }

    private static final int NUM_ITEMS = 5;

    public static boolean isSorted(IntContainer a[]) {
        for(int i = a.length - 1; i > 0; i--)
            if(a[i].value < a[i-1].value)
                return false;

        return true;
    }

    public static void main(String[] args)
    {
        int j = 1;

        IntContainer[] a = new IntContainer[NUM_ITEMS];
        Random randomGenerator = new Random();
        for(int i = 0; i < a.length; i++)
            a[i] = new IntContainer(randomGenerator.nextInt());

        Sort.quicksort(a);

        for (int i = 0; i < a.length; i++)
            System.out.println(a[i].value);

        if (!isSorted(a))
            j = j / 0;
   }
}

11 More information

For more information on LCT:

  1. The course's slides1 on Static and Dynamic Symbolic Execution and In the spotlight: the Lime Concolic Tester present the material covered in this exercise session.
  2. The user guide of Lime2 presents the concolic tester that we have seen in this exercise session, but also the monitoring features of Lime.
  3. LCT: An open source concolic testing tool for Java programs, Kähkönen et al.3 This short paper discusses the design of LCT.
  4. LCT: A parallel distributed testing tool for multithreaded Java programs, Kähkönen et al.4 This paper specifically discusses how LCT handles multi-threading in the programs it analyzes.
  5. Automated Test Generation for Software Components, Kähkönen5. This technical report is used as an inspiration for this exercise session.

Footnotes:

1

: http://soft.vub.ac.be/~cderoove/software_quality/

2

: http://www.tcs.hut.fi/Software/lime/userguide.pdf

3

: http://users.ics.aalto.fi/ktkahkon/KahLauSaaKauHelNie-BYTECODE2011.pdf

4

: http://users.ics.aalto.fi/kepa/publications/lct-pdmc-final.pdf

5

: http://users.ics.aalto.fi/ktkahkon/TKK-ICS-R26.pdf

Last update: 2015-10-09T12:33:53+02:00