Higher-Order Programming » Lab Sessions

Session 3

Assistant: Steven Keuchel (steven.keuchel@vub.be)

Section 1: Pairs

The simplest compound datatype in Scheme is a pair of two values. The cons procedure takes two arguments and creates a new pair, where the first argument will be stored as the first component of the pair, and the second argument as the second component.

(define a (cons 1 2))

Pairs and other compound datatypes can be visualized by so-called box-and-pointer diagrams. For instance the pair a defined above is represented by the following diagram:

To access the individual components of the pair, you can use car and cdr. car will get the value stored at the first component, cdr the second component.

(car a) ; -> 1 (cdr a) ; -> 2

The predicate procedure pair? tests if a given value is a pair.

(pair? a) ; -> #t (pair? 2) ; -> #f

Exercise 1.1: Swapping

Define a function swap that takes a pair and produces a new pair, where the elements are exchanged.

(swap (cons 1 2)) ; -> (2 . 1) (swap (cons "a" "b")) ; -> ("b" . "a)

Exercise 1.2: Pair Ordering

Define a function sort-pair that takes a pair of two numbers and produces a new pair where the components are ordered, i.e. the left component is smaller or equal to the right component.

(sort-pair (cons 10 15)) ; -> (10 . 15) (sort-pair (cons 3.1 2)) ; -> (2 . 3.1)

Exercise 1.3: Pair Mapping

Define a function map-pair that takes three parameters: two functions l and r and a pair x. map-pair should apply l to the left component of x and r to the right component of x and produce a new pair.

(map-pair number? odd? (cons "abc" 3)) ; -> (#f . #t) (map-pair (lambda (s) (string-append s "!")) (lambda (l) (cons (length l) l)) (cons "Hi" '(4 5 6))) ; -> ("Hi!" 3 4 5 6)

Exercise 1.4: Pair Folding

Define a function fold-pair that takes two parameters:

• a two-parameter function c, and
• a pair x. Fold-pair should apply c to the components of x.

(fold-pair + (cons 10 15)) ; -> 25 (fold-pair string-append (cons "Hello, " "World!")) ; -> "Hello, World!"

Exercise 1.5: Folding revisited

Write swap, sort-pair and map-pair in terms of fold-pair.

(define (swap2 x) (fold-pair .... x))

Section 2: Trees and lists

Pairs are not limited to primitive datatypes, but can store other compound datatypes (e.g., other pairs). The following is a diagram of (cons a 5).

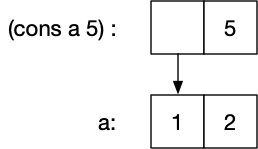
The following structures are all identical, the first one is the canonical form.

'(1 2 3 4) '(1 . (2 3 4)) '(1 . (2 . (3 4))) '(1 . (2 . (3 . (4)))) '(1 . (2 . (3 . (4 . ())))) ; ' is used for literal notation. ; I.e., '(a b) is not the application of a with b as an argument. ; It is the list data structure storing two symbols: 'a and 'b.

'() refers to the empty list. You can check for the empty list using (null? p).

All these structures have the following box-and-pointer diagram.

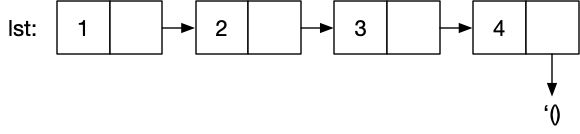
The procedure list builds a list of values.

(list 1 2 3 4) ; -> '(1 2 3 4)

Exercise 2.1: Simple box-and-pointer diagram

Using pen and paper, draw a box-and-pointer diagram of the following structure.

(cons 1 (cons 2 (cons 3 4)))

Exercise 2.2: Advanced box-and-pointer diagrams

Using pen and paper, draw a box-and-pointer diagram of the following structures. Explain the type of each structure (e.g., is it a tree? is it a list?).

; a) (cons 1 (cons 2 '())) ; b) (list 1 2 3 4) ; c) (cons 'vub (list (cons 'we (list 'dinf 'surf)) (cons 'gf (list 'farm 'gero)))) ; d) (cons 1 (cons 2 3)))

Exercise 2.3: Shared memory in box-and-pointer-diagrams

Using pen and paper, draw a single box-and-pointer diagram of all the variables occuring in this program. What is shown when displaying every variable?

(define a (list 1 2 3)) (define b (car a)) (define c (cdr a)) (define d (cons 4 c)) (define e (cons 5 '())) (define f (cons a e)) (define g (cddr a))

Hint! Refer to the report on R5RS to find out what the semantics of cddr are.

As the box-and-pointer diagrams suggest, compound datatypes in a pair are stored by reference, not by copy. It is possible to modify the value stored in a pair via set-car! and set-cdr! (for usage, refer to the documentation).

What happens when evaluate (set-cdr! c 'apple) afterwards? What is changed when you display every variable again?

Section 3: Higher-Order Procedures on Lists

In this course, we will make use of higher-order procedures, which are procedures that take a first-class procedure as argument.

Exercise 3.1: Sum

In this exercise, we will implement multiple versions of a sum procedure, that calculates the sum of all elements in a given list structure.

1. Implement sum using recursion.
2. Implement the higher-order procedure accumulate that has three parameters: a procedure, a default value, and a list.
3. Implement sum by making use of accumulate

For the first part, use the following boilerplate code.

(define (sum lst) (if (null? lst) ... (+ ... (sum ...))))

Exercise 3.2: Filtering

Complete the following definition of filter.

(define (filter predicate lst) (cond ((null? ...) '()) ((predicate ...) (cons ... (filter predicate ...))) (else ...)))

Then, call filter on the list '(4 8 15 16 23 42) such that only odd numbers are kept.

Then, create a predicate that matches positive odd numbers. And pass this predict to filter the following list: (1 -1 2 -3 5 -8 13 -21 34 -55 89).

Hint! As a convention in Scheme, all names for predicate procedures should end on ? (e.g., even?, pair?,...)

Exercise 3.3: Reversing Lists

The reverse function takes a list and reverses the order of the elements:

(reverse (list 1 2 3)) ; -> (3 2 1)

Implement your own version of reverse. Hint! Write a function with an iterative process.

Section 4: Higher-Order Procedures on Trees

For the exercises in this section, we will use the following trees.

(define tree-a (cons (cons 1 2) 3)) (define tree-b (cons 1 (cons (cons 2 (cons 3 '())) (cons (cons 4 (cons 5 6)) (cons 7 '()))))) (define tree-c (cons (cons 1 2) (cons 3 4)))

If you feel stuck on one of these exercises, it can help to draw either a box-and-pointer diagram, or a tree diagram of these structures.

Exercise 4.1: Sum and depth of a tree

First, write a procedure that calculates the sum of all numbers in a tree, and the depth of a tree. If you are stuck, check the implementation of count-leaves given during the theory (Chapter 2, Slide 22).

Predict what will happen if you pass the given trees to your procedures, then apply this procedure on all given trees. Did your outcome match your expectations?

Second, write a generic procedure that processes all elements in a tree. Complete the following boilerplate code. The intuition behind the three parameters is as follows:

• combiner is a two-parameter function that combines two values of the result domain.
• f is a one-parameter function that maps a single element to the result domain.
• neutral is a value that represents a neutral element of the combiner function.

(define (fold-tree combiner neutral f tree) (cond (<???> neutral) ((not (pair? tree)) <???>) (else (<???> (fold-tree combiner neutral f <???>) (fold-tree combiner neutral f <???>)))))

Third, write your procedures of the first part of this exercise using fold-tree and verify whether you get the same result.

Exercise 4.2: Mapping the values on a tree.

Write a procedure tree-map that maps all the values in a tree according to some mapper function. Can you make use of fold-tree from the previous exercise to implement tree-map? If so, implement this variant.

Bonus Exercises

Bonus Exercise 1: Cycle

Recommended after exercise 3

Write a procedure that takes 3 arguments, and builds a cycle structure. E.g., the result of executing (make-cycle 8 5 3) should look like:

What is the output of when you display a data structure with a cyclic dependency?

Bonus Exercise 2: Generic Function Composition

Recommended after exercise 5

In the previous exercise session you have implemented compose for function composition. In the theory you have seen something that should make it possible to implement compose such that it can be executed on a dynamic number of arguments. Improve your implementation of compose such that it has support for multiple parameters.

Tip! Check section 4.1.4 of the R5RS manual for the different syntactical options for <Formals>.