Introduction
All solutions and tests for session 3: ex3solution.pde
Exercises
Exercise 1: Clipping lines - determining whether 2 lines intersect
int calcSign(Point p1, Point p2, Point a) {
// return: 0 on line
// + pos side
// - neg side
return (a.y-p1.y)*(p2.x-p1.x) - (a.x-p1.x)*(p2.y-p1.y);
}
// note: does not work if p1-p2 and p3-p4 are collinear (lie on the same line)
boolean linesIntersect(Point p1, Point p2, Point p3, Point p4) {
// 2 vertical lines lying on the same line?
if ((p1.x == p2.x) && (p3.x == p4.x) && (p1.x == p3.x)) {
return ((p1.y <= p3.y) && (p3.y <= p2.y)) || ((p3.y <= p1.y) && (p1.y <= p4.y));
// 2 horizontal lines lying on the same line?
} else if ((p1.y == p2.y) && (p3.y == p4.y) && (p1.y == p3.y)) {
return ((p1.x <= p3.x) && (p3.x <= p2.x)) || ((p3.x <= p1.x) && (p1.x <= p4.x));
}
int s1 = calcSign(p1, p2, p3);
int s2 = calcSign(p1, p2, p4);
int s3 = calcSign(p3, p4, p1);
int s4 = calcSign(p3, p4, p2);
return ((s1*s2<=0) && (s3*s4<=0));
}
Exercise 2: Clipping lines - determining the intersection point
/** @return intersection Point or null */
Point calcIntersection(Point p1, Point p2, Point p3, Point p4) {
int n;
double x, y;
int a = p1.y-p2.y; // y1 - y2
int b = p2.x-p1.x; // x2 - x1
int c = p1.y*p2.x - p2.y*p1.x; // y1*x2 - y2*x1
int d = p3.y-p4.y;
int e = p4.x-p3.x;
int f = p3.y*p4.x - p4.y*p3.x;
if ((n=a*e-b*d)==0) return null; // lines parallel
x = (c*e-b*f)/(double)n;
if ((x>p1.x) && (x>p2.x)) return null; // intersection outside segment
if ((x<p1.x) && (x<p2.x)) return null;
if ((x>p3.x) && (x>p4.x)) return null;
if ((x<p3.x) && (x<p4.x)) return null;
y = (a*f-c*d)/(double)n;
return new Point( (int)x, (int)y );
}
Exercise 3: clipping in the plane - the Cohen-Sutherland algorithm
// 4 bits to represent whether a point lies to left, right,
// bottom or top of the clipping window
private static final int LEFT = 1<<0;
private static final int RIGHT = 1<<1;
private static final int BOTTOM = 1<<2;
private static final int TOP = 1<<3;
private static int computeCode(int x, int y, int xmin, int xmax, int ymin, int ymax) {
int code = 0;
if (y > ymax)
code = TOP;
else if (y < ymin)
code = BOTTOM;
if (x > xmax)
code |= RIGHT;
else if (x < xmin)
code |= LEFT;
return code;
}
/** @return the clipped line or null if it lies completely out of the rectangle */
private static Line cohenSutherlandClip(
int x0, int y0, int x1, int y1,
int xmin, int xmax, int ymin, int ymax) {
int x = 0;
int y = 0;
int outcode0, outcode1, outcode;
outcode0 = computeCode(x0, y0, xmin, xmax, ymin, ymax);
outcode1 = computeCode(x1, y1, xmin, xmax, ymin, ymax);
while (true) {
if ((outcode0 | outcode1) == 0) {
// both endpoints have code 0000: trivial accept and exit
return new Line(new Point(x0, y0), new Point(x1, y1));
}
if ( (outcode0 & outcode1) != 0 ) {
// both endpoints lie in one of the outer areas and do not
// cross the clipping window: trivial reject
return null;
}
if (outcode0 != 0)
// x0,y0 lies outside rectangle
outcode = outcode0;
else
// x1,y1 lies outside rectangle
outcode = outcode1;
// find an intersection point with clipping window
if ((outcode & TOP) != 0) {
// x-coord at maximal y
x = x0 + (x1-x0) * (ymax-y0) / (y1-y0);
y = ymax;
} else if ((outcode & BOTTOM) != 0) {
// x-coord at minimal y
x = x0 + (x1-x0) * (ymin-y0) / (y1-y0);
y = ymin;
} else if ((outcode & RIGHT) != 0) {
// y-coord at maximal x
y = y0 + (y1-y0) * (xmax-x0) / (x1-x0);
x = xmax;
} else if ((outcode & LEFT) != 0) {
// y-coord at minimal x
y = y0 + (y1-y0) * (xmin-x0) / (x1-x0);
x = xmin;
}
// move outside point to intersection point to clip
// also get ready for next iteration
if (outcode == outcode0) {
x0 = x;
y0 = y;
outcode0 = computeCode(x0,y0,xmin,xmax,ymin,ymax);
} else {
x1 = x;
y1 = y;
outcode1 = computeCode(x1,y1,xmin,xmax,ymin,ymax);
}
}
}
Exercise 4: Point inside polygon
General way of determining whether a point lies within a polygon: draw a horizontal line through the point and determine all intersections with the polygon. When going through those points left to right, we start outside of the polygon. Passing the first intersection point, we enter the polygon, until we reach the second intersection point, etc. A point lies within the polygon if the number of intersection points to the left of the point is odd.
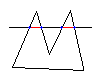
There are, however, some border cases, when the horizontal line crosses a vertex of the polygon or when the polygon contains a horizontal side that lies on top of our horizontal line.
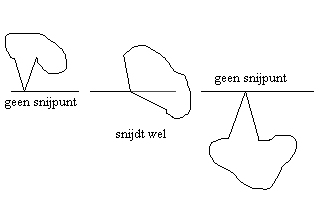
Solution: do not count all intersection points but only those where the polygon continues below. We only count the "-" signs on the following figure. When the number of "-" signs is odd, the point lies within the polygon. We can consider this method as clipping the polygon at the horizontal line.
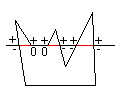
public boolean containsPointWernerDeluxe(Point p) {
Point p1, p2;
int count=0;
p2=(Point)poly.get(0);
for (int i=0; i<poly.size(); i++) {
p1=p2;
p2 = (Point)poly.get((i+1)%poly.size());
if (((p.y>p1.y) && (p.y>p2.y)) || ((p.y<p1.y) && (p.y<p2.y)))
continue; // snijd niet
if (p1.y==p2.y) // horz lijn
if ((p.x-p1.x)*(p.x-p2.x)<=0) // return als punt op horz lijn ligt
return true;
else continue;
if (Math.max(p1.y, p2.y) == p.y) continue; // 0 op tekening
if ((p.y-p1.y)*(p2.x-p1.x)/(double)(p2.y-p1.y) < (p.x-p1.x)) // snijdt
count++;
}
return (count%2)==1;
}