7.8
11 Bomen
Geneste Lijsten
11.1 Recursie/iteratie op geneste lijsten: modeloplossing
Het volgende stukje "pseudo-code" beschrijft een standaardpatroon van een boomrecursieve procedure.
Bijna elke boomrecursieve procedure zal geschreven zijn volgens dit patroon, of een zeer sterk gelijkend patroon.
| (define (atom? x) |
| (not (pair? x))) |
| |
| (define (tree-procedure-rec lst) |
| (cond ((null? lst) base-result) |
| ((atom? lst) atom-result) |
| (else (combine-branches (tree-procedure-rec (car lst)) |
| (tree-procedure-rec (cdr lst)))))) |
11.2 Diepte en bladeren van een boom
We weten dat we een boom kunnen voorstellen d.m.v. een geneste lijst.
11.2.1 Aantal elementen van een boom
Schrijf een procedure (leaf-count tree) die het aantal elementen (= bladeren) in
zo’n boom telt.
| (define (leaf-count tree) | | (cond | | ((null? tree) 0) | | ((atom? tree) 1) | | (else (+ (leaf-count (car tree)) | | (leaf-count (cdr tree)))))) |
|
|
|
| > (leaf-count '((1 2) ((3 4) 5) (6 7))) |
7 |
11.2.2 Diepte van een boom
Schrijf een procedure depth die de nesting-diepte van een boom
berekent. M.a.w. hoeveel haakjes staan er rond het meest geneste
element van de boom?
| (define (depth tree) | | (cond ((null? tree) 0) | | ((atom? tree) 0) | | (else (max (+ 1 (depth (car tree))) | | (depth (cdr tree)))))) |
|
|
|
| > (depth '((1 2) ((3 4) 5) (6 7))) |
3 |
11.2.3 Diepte en aantal elementen van een boom
Schrijf een procedure die (a) en (b) combineert, maar zo efficiënt
mogelijk. D.w.z. de boom mag maar 1 enkele keer volledig doorlopen
worden.
| (define (depth-and-leaf-count tree) | | (define make-res cons) | | (define depth car) | | (define leaf-count cdr) | | | | (cond | | ((null? tree) (make-res 0 0)) | | ((atom? tree) (make-res 0 1)) | | (else (let ((res-car (depth-and-leaf-count (car tree))) | | (res-cdr (depth-and-leaf-count (cdr tree)))) | | (make-res (max (+ 1 (depth res-car)) | | (depth res-cdr)) | | (+ (leaf-count res-car) | | (leaf-count res-cdr))))))) |
|
|
|
| > (depth-and-leaf-count '((1 2) ((3 4) 5) (6 7))) |
(3 . 7) |
11.3 fringe
Deze oefening is gebaseerd op oefening 2.28 van
Structure
and Interpretation of Computer Programs
Definieer de procedure (fringe l) die een lijst teruggeeft
met alle atomen van een diepgeneste lijst.
| (define (fringe l) | | (cond ((null? l) '()) | | ((atom? l) (list l)) | | (else (append (fringe (car l)) | | (fringe (cdr l)))))) |
|
|
|
| > (fringe '((1) ((((2)))) (3 (4 5) 6) ((7) 8 9))) |
(1 2 3 4 5 6 7 8 9) |
11.4 Structuur vergelijken
Definieer het predicaat (same-structure? l1 l2), dat nagaat
of twee lijsten op de atomen na dezelfde structuur hebben. Hou
rekening met dotted-pairs.
| (define (same-structure? l1 l2) | | (cond ((and (null? l1) (null? l2)) #t) | | ((or (null? l1) (null? l2)) #f) | | ((and (atom? l1) (atom? l2)) #t) | | ((or (atom? l1) (atom? l2)) #f) | | (else (and (same-structure? (car l1) (car l2)) | | (same-structure? (cdr l1) (cdr l2)))))) | | | | (define (same-structure?-or l1 l2) | | (or (and (null? l1) (null? l2)) | | (and (atom? l1) (atom? l2)) | | (and (pair? l1) | | (pair? l2) | | (same-structure?-or (car l1) (car l2)) | | (same-structure?-or (cdr l1) (cdr l2))))) |
|
|
|
| > (same-structure? '((1 2) ((3 . 4) ((5 6) ((7 8) (9))))) | | '((a b) ((c . d) ((e f) ((g h) (i)))))) |
|
#t |
| > (same-structure? '((1 2) ((3 4) ((5 6) ((7 8) (9))))) | | '((((1 2) (3 4)) ((5 6) (7 8))) 9)) |
|
#f |
11.5 Hogere Orde: deep-combine en deep-map
11.5.1 Deep-combine
Definieer de functie (deep-combine combiner null-value l),
die alle atomen van een (eventueel geneste) lijst combineert.
| (define (deep-combine combiner null-value l) | | (cond ((null? l) null-value) | | ((atom? l) l) | | (else (combiner (deep-combine combiner | | null-value | | (car l)) | | (deep-combine combiner | | null-value | | (cdr l)))))) |
|
|
|
| > (deep-combine + 0 '((((1 2) (3 4)) ((5 6) (7 8))) 9)) |
45 |
11.5.2 Deep-map
Definieer de functie (deep-map f l),
die als resultaat een lijst teruggeeft met dezelfde structuur
als l, maar waarin alle atomen vervangen zijn door het
resultaat van f op het atoom.
| (define (deep-map f l) | | (cond | | ((null? l) '()) | | ((atom? l) (f l)) | | (else (cons (deep-map f (car l)) | | (deep-map f (cdr l)))))) |
|
|
|
| > (deep-map (lambda (x) (* x x)) | | '((((1 . 2) (3 4)) ((5 6) (7 8))) . 9)) |
|
((((1 . 4) (9 16)) ((25 36) (49 64))) . 81) |
11.5.3 Deep-change
Definieer (deep-change e1 e2 l), aan de hand van
deep-map en/of deep-combine,
die een lijst terug met dezelfde structuur als l,
maar alle atomen e1 verandert in e2.
| (define (deep-change e1 e2 l) | | (deep-map (lambda (e) (if (eq? e e1) e2 e)) l)) |
|
|
|
| > (deep-change 3 999 '((((1 . 2) (3 4)) ((5 6) (7 8))) . 9)) |
((((1 . 2) (999 4)) ((5 6) (7 8))) . 9) |
11.5.4 Deep-atom-member?
Definieer (deep-atom-member? e l), aan de hand van
deep-map en/of deep-combine,
die kijkt of e (een atoom) ergens in een geneste
lijst voorkomt.
| (define (deep-atom-member? e l) | | (deep-combine (lambda (car cdr) (or car cdr)) | | #f | | (deep-map (lambda (x) (eq? e x)) l))) |
|
|
|
| > (deep-atom-member? 3 '((((1 . 2) (3 4)) ((5 6) (7 8))) . 9)) |
#t |
| > (deep-atom-member? 999 '((((1 . 2) (3 4)) ((5 6) (7 8))) . 9)) |
#f |
11.5.5 Count-atoms
Definieer (count-atoms l), aan de hand van
deep-map en/of deep-combine,
die het aantal atomen in een lijst telt.
| (define (count-atoms l) | | (deep-combine + 0 (deep-map (lambda (x) 1) l))) |
|
|
|
| > (count-atoms '((((1 . 2) (3 4)) ((5 6) (7 8))) . 9)) |
9 |
11.6 Examen Informatica Partieel januari 1995
Het laboratorium voor biotechnologie aan de VUB probeert een soort
hybride appelboom te ontwikkelen waarop verschillende soorten appels
kunnen groeien. Elke tak van zo’n boom kan vertakken in een nieuwe
tak, maar er kunnen ook 1 of meerdere bladeren en/of appels aan
hangen. Hieronder vind je een voorbeeld van zo’n boom.
Om de biologische eigenschappen van deze nieuwe boomsoort te voorspellen
contacteren de onderzoekers het departement informatica om er een
computermodel voor te ontwikkelen.
In dit model zal de appelboom worden voorgesteld als een diepgeneste lijst.
De bovenstaande boom ziet er in het model bijvoorbeeld als volgt uit:
| (define boom | | '((blad (appel . golden)) | | (blad (appel . granny)) | | (((appel . golden) blad) blad (appel . cox)))) |
|
|
|
11.6.1 Tel bladeren
Schrijf een procedure (leafs boom) die het aantal bladeren in zo’n
appelboom kan tellen.
| (define (blad? boom) | | (eq? boom 'blad)) | | | | (define (appel? boom) | | (and (pair? boom) (eq? (car boom) 'appel))) | | | | (define (type appel) (cdr appel)) | | | | (define (leafs boom) | | (cond ((null? boom) 0) | | ((blad? boom) 1) | | ((appel? boom) 0) | | (else (+ (leafs (car boom)) | | (leafs (cdr boom)))))) |
|
|
|
11.6.2 Zoek alle appels
Schrijf een procedure (all-apples boom) die een lijstje maakt van alle appels die
in een gegeven appelboom voorkomen.
| (define (all-apples boom) | | (cond ((null? boom) '()) | | ((blad? boom) '()) | | ((appel? boom) (list (type boom))) | | (else (append (all-apples (car boom)) | | (all-apples (cdr boom)))))) |
|
|
|
| > (all-apples boom) |
(golden granny golden cox) |
11.6.3 Geef de verschillende soorten appels
Schrijf een procedure
(apple-types boom) die een lijstje maakt van alle soorten
appels die in een gegeven appelboom voorkomen. Het verschil met
(all-apples boom) zit hem in het feit dat je nu geen dubbels
in de resultaatlijst wil.
Hint: beschouw de lijsten als verzamelingen zoals je deze kent uit de
wiskunde.
| (define (union l1 l2) | | (cond | | ((null? l1) l2) | | ((member (car l1) l2) (union (cdr l1) l2)) | | (else (cons (car l1) (union (cdr l1) l2))))) | | | | (define (apple-types boom) | | (cond ((null? boom) '()) | | ((blad? boom) '()) | | ((appel? boom) (list (type boom))) | | (else (union (apple-types (car boom)) | | (apple-types (cdr boom)))))) |
|
|
|
| > (apple-types boom) |
(granny golden cox) |
11.6.4 Procedure om de boom te bewerken
Schrijf een hogere-orde procedure
(bewerk-boom boom doe-blad doe-appel combiner init)
die je in het algemeen kan gebruiken om een appelboom te bewerken.
| (define (bewerk-boom boom doe-blad doe-appel combiner init) | | (cond | | ((null? boom) init) | | ((blad? boom) (doe-blad boom)) | | ((appel? boom) (doe-appel boom)) | | (else (combiner | | (bewerk-boom (car boom) doe-blad doe-appel combiner init) | | (bewerk-boom (cdr boom) doe-blad doe-appel combiner init))))) |
|
|
|
11.6.5 Tel bladeren (hogere orde)
Herschrijf (leafs boom) d.m.v. bewerk-boom.
Noem deze versie (leafs-dmv-bewerk boom).
| (define (leafs-dmv-bewerk boom) | | (bewerk-boom boom | | (lambda (blad) 1) | | (lambda (appel) 0) | | + | | 0)) |
|
|
|
| > (leafs-dmv-bewerk boom) |
4 |
11.6.6 Geef alle appels (hogere orde)
Herschrijf all-apples d.m.v. bewerk-boom.
Noem deze versie (all-apples-dmv-bewerk boom).
| (define (all-apples-dmv-bewerk boom) | | (bewerk-boom boom | | (lambda(blad) '()) | | (lambda(appel) (list (type appel))) | | append | | '())) |
|
|
|
| > (all-apples-dmv-bewerk boom) |
(golden granny golden cox) |
11.6.7 Geef de verschillende soorten appels (hogere orde)
Herschrijf apple-types d.m.v. bewerk-boom.
Noem deze versie (all-types-dmv-bewerk boom).
| (define (apple-types-dmv-bewerk boom) | | (bewerk-boom boom | | (lambda(blad) '()) | | (lambda(appel) (list(type appel))) | | union | | '())) |
|
|
|
| > (apple-types-dmv-bewerk boom) |
(granny golden cox) |
11.7 Circulaire Datastructuren: cycles?
Deze oefening is gebaseerd op oefening 3.18 van
Structure
and Interpretation of Computer Programs
Schrijf een predicaat (cycles? r) dat zegt of r een
cyclus bevat (d.w.z. dat het aflopen van de lijst door opeenvolgende
cdr’s in een oneindige loop raakt).
| (define (cycles? lst) | | (define (find-cycles? current path) | | (cond | | ((null? current) #f) | | ((memq current path) #t) | | (else (find-cycles? (cdr current) | | (cons current path))))) | | (find-cycles? lst '())) |
|
|
|
| > (define car-loop | | (let ((first (cons 'a '()))) | | (set-car! first first) | | first)) |
|
| > (cycles? car-loop) |
#f |
| > (define ring | | (let* ((last (cons '3 '())) | | (list (cons 1 (cons 2 last)))) | | (set-cdr! last list) | | list)) |
|
| > (cycles? ring) |
#t |
11.8 Oefening 3.16 uit Abelson&Sussman
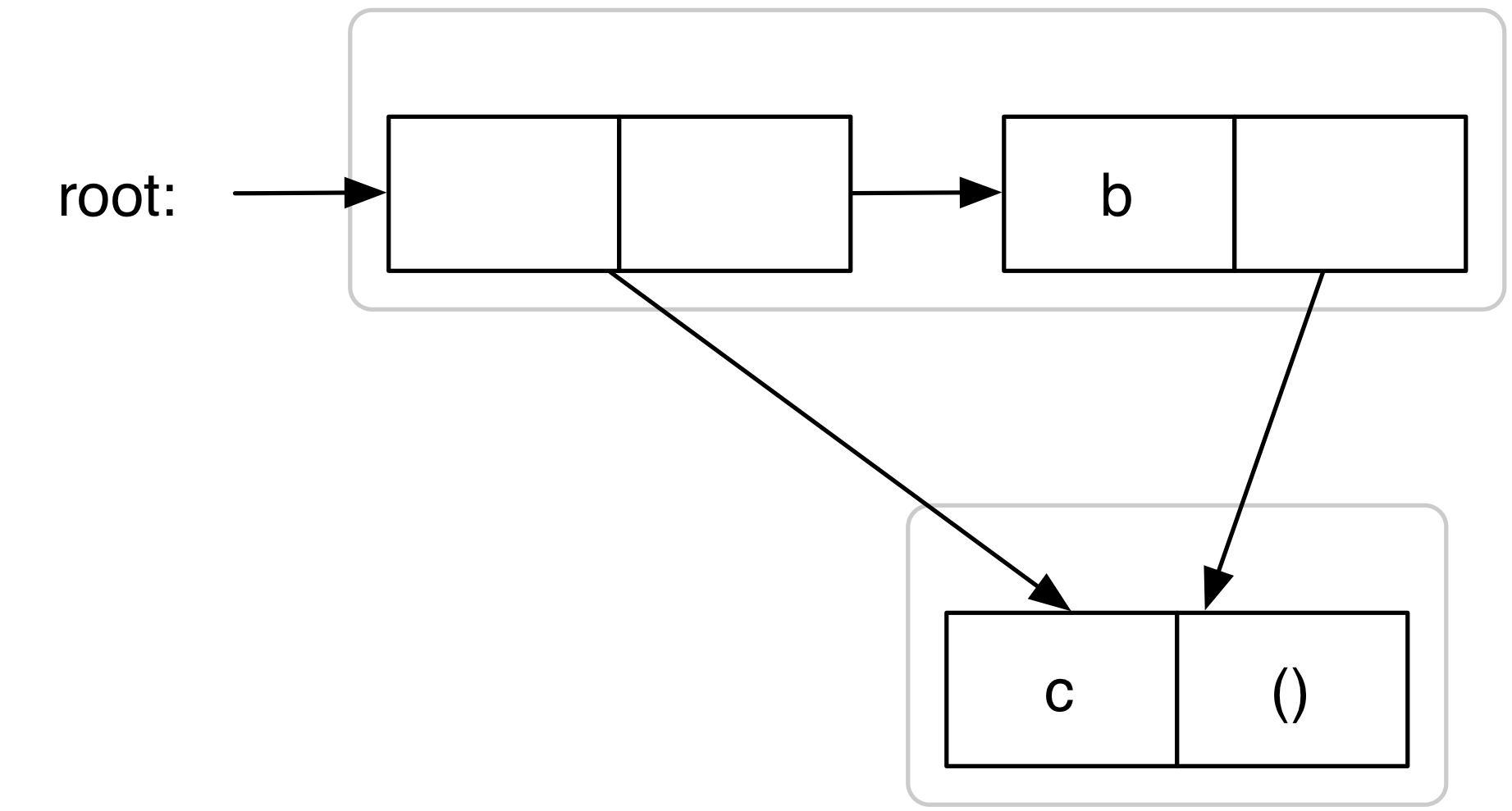
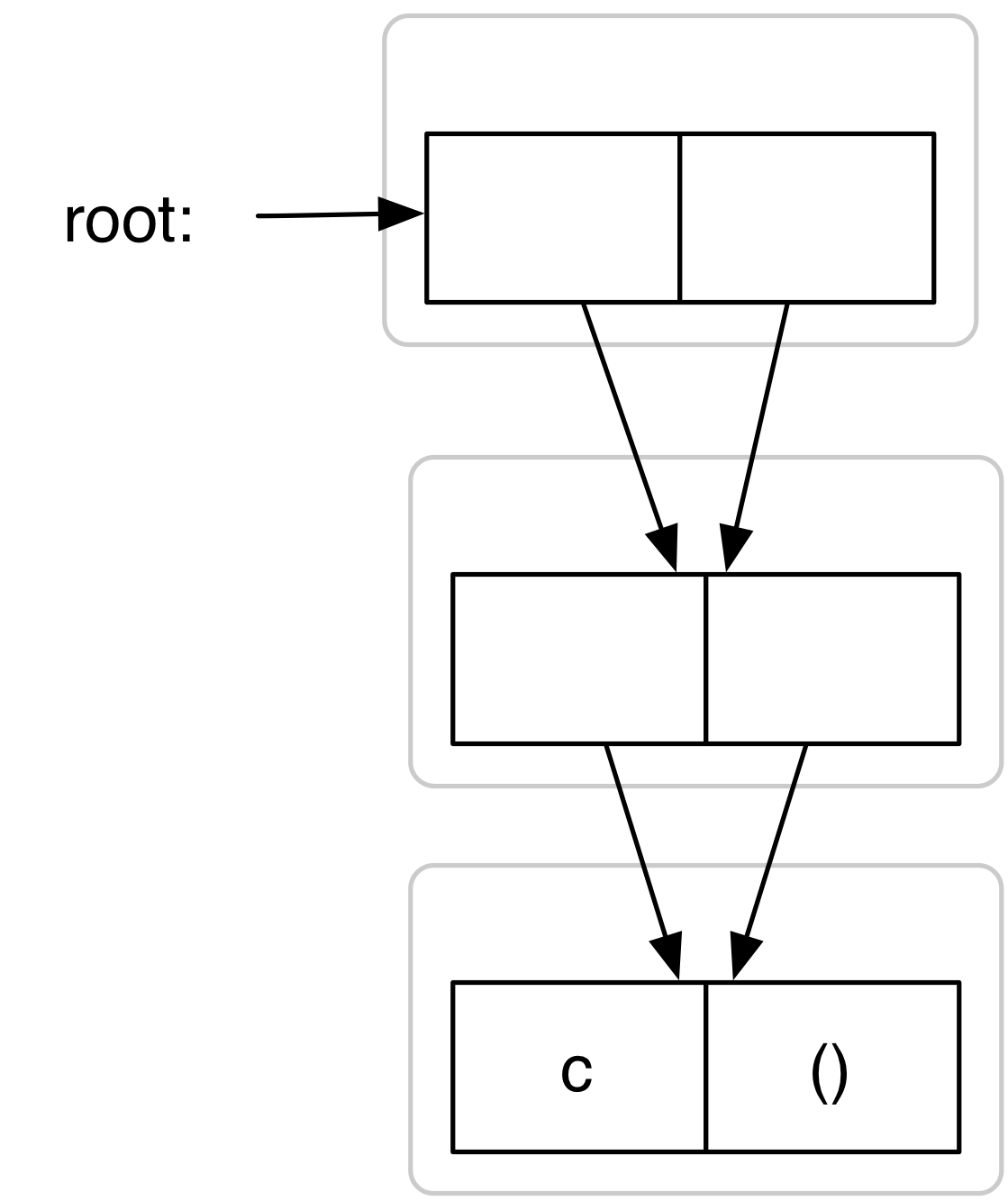
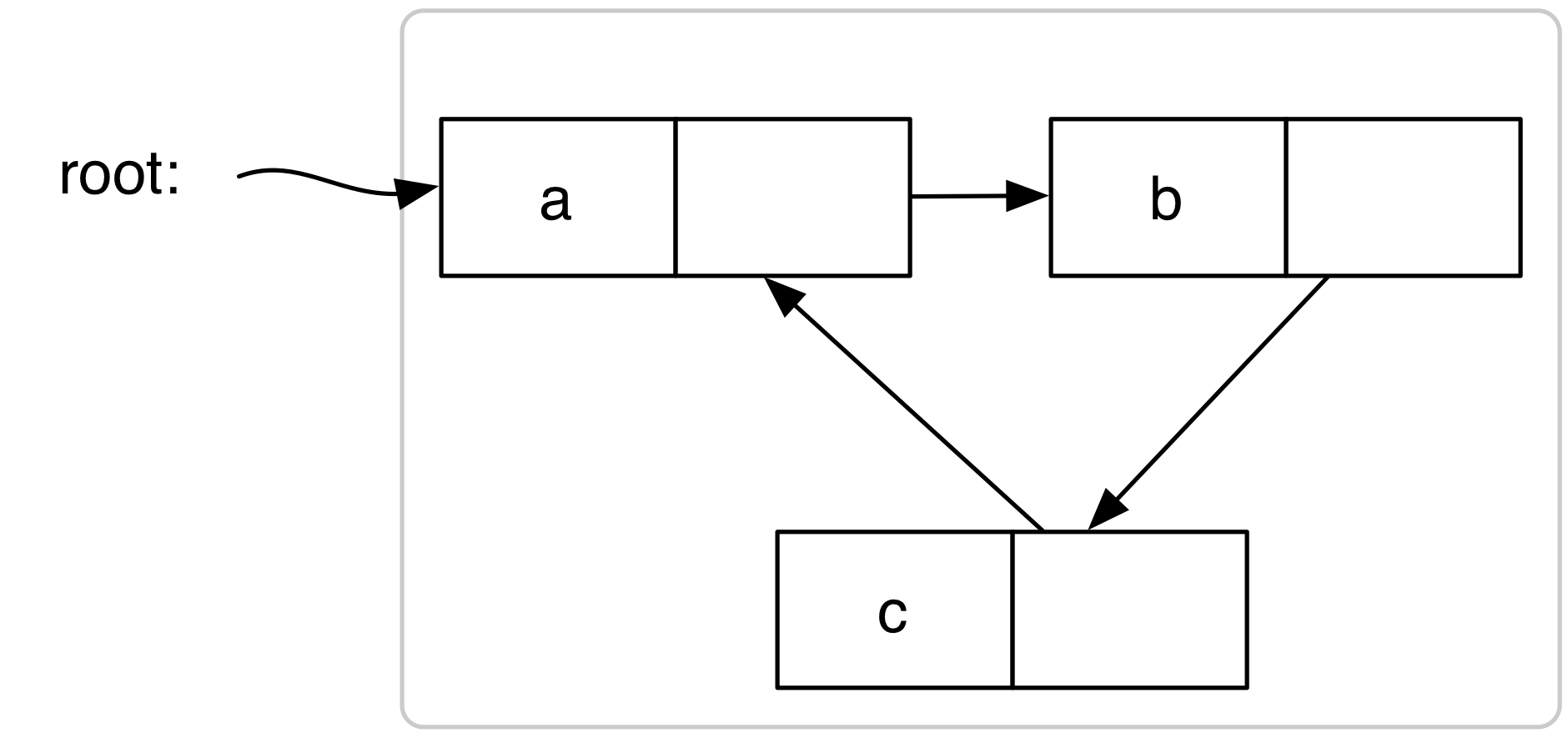
Je wil een functie schrijven die het aantal cons-cellen in een structuur telt. Toon aan dat onderstaande procedure count-pairs niet het gewenste resultaat geeft door box-pointer diagrammen met 3 cellen te tekenen, waarvoor het resultaat van count-pairs respectievelijk resulteert in 3, 4, 7 en een oneindige lus. Schrijf expressies om die structuren te maken.
| (define (count-pairs x) | | (if (not (pair? x)) | | 0 | | (+ (count-pairs (car x)) | | (count-pairs (cdr x)) | | 1))) |
|
|
|
| (define ret3 (cons 'a (cons 'b (cons 'c '())))) |
|
|
| (define ret4 | | (let ((last (cons 'c '()))) | | (cons last (cons 'b last)))) |
|
|
|
| (define ret7 | | (let* ((last (cons 'c '())) | | (middle (cons last last))) | | (cons middle middle))) |
|
|
|
| (define retno | | (let* ((last (cons 'c '())) | | (lst (cons 'a (cons 'b last)))) | | (set-cdr! last lst) | | lst)) |
|
|
|
Geen resultaat; oneindige lus
11.9 Correcte versie count-pairs
Schrijf een correcte versie van de procedure count-pairs die
het aantal verschillende cons-cellen teruggeeft.
Hint: hou een extra lijst bij van reeds getelde cons-cellen.
| (define (count-pairs lst) | | (let ((path '())) | | (define (count current) | | (cond | | ((null? current) 0) | | ((not (pair? current)) 0) | | ((memq current path) 0) | | (else | | (set! path (cons current path)) | | (+ 1 (count (car current)) | | (count (cdr current)))))) | | (count lst))) |
|
|
|
| > (define ret3 (cons 'a (cons 'b (cons 'c '())))) |
| > (count-pairs ret3) |
3 |
| > (define ret4 | | (let ((last (cons 'c '()))) | | (cons last (cons 'b last)))) |
|
| > (count-pairs ret4) |
3 |
| > (define ret7 | | (let* ((last (cons 'c '())) | | (middle (cons last last))) | | (cons middle middle))) |
|
| > (count-pairs ret7) |
3 |
| > (define retno | | (let* ((last (cons 'c '())) | | (lst (cons 'a (cons 'b last)))) | | (set-cdr! last lst) | | lst)) |
|
| > (count-pairs retno) |
3 |
11.10 Geneste Lijsten: Extra Oefeningen
11.10.1 unfringe
Definieer de procedure (unfringe l) die een platte lijst als
argument neemt en een lijst teruggeeft die, net als al haar
sublijsten, maximaal 2 elementen telt en terug l geeft als je
er fringe (uit vraag 3) op los laat.
Vermits verschillende lijsten hetzelfde resultaat kunnen
opleveren met fringe, is het resultaat van unfringe niet eenduidig
bepaald. Wij geven twee opties, die we unfringe-1 en unfringe-2 hebben genoemd.
Implementeer één van de twee opties, maar definieer uw procedure als (unfringe l).
Dit is belangrijk voor het automatisch testen.
Eerste manier:
| (define (unfringe-1 l) | | (cond ((null? l) '()) | | ((null? (cdr l)) (list (car l))) | | (else (list (car l) | | (unfringe-1 (cdr l)))))) |
|
|
|
Tweede manier:
| (define (unfringe-2 l) | | (define (pair l) | | (cond ((null? l) '()) | | ((null? (cdr l)) (list l)) | | (else (cons (list (car l) (cadr l)) | | (pair (cddr l)))))) | | | | (let loop ((l l)) | | (if (or (null? l) | | (null? (cdr l))) | | l | | (loop (pair l))))) |
|
|
|
| > (unfringe-1 '(1 2 3 4 5 6 7 8 9)) |
(1 (2 (3 (4 (5 (6 (7 (8 (9))))))))) |
| > (unfringe-2 '(1 2 3 4 5 6 7 8 9)) |
(((((1 2) (3 4)) ((5 6) (7 8))) (((9))))) |
11.10.2 Hogere Orde: tree-accumulate
11.10.2.1 Implementeer
Definieer de hogere orde functie (tree-accumulate tree term combiner null-value), die werkt zoals accumulate uit reeks
4. De tree-accumulate procedure past de procedure
term enkel toe op atomen, en gebruikt de combiner
procedure om de accumulatie van de deellijsten te combineren.
| (define (tree-accumulate tree term combiner null-value) | | (cond ((null? tree) null-value) | | ((atom? tree) (term tree)) | | (else (combiner (tree-accumulate (car tree) | | term | | combiner | | null-value) | | (tree-accumulate (cdr tree) | | term | | combiner | | null-value))))) |
|
|
|
| > (tree-accumulate '(9 ((9 9)) (((9 9))) (9)) | | (lambda (x) 1) | | + | | 0) |
|
6 |
11.10.2.2 Hergebruik
Definieer fringe, deep-combine en deep-map aan de hand van tree-accumulate.
| (define (fringe l) | | (tree-accumulate l list append '())) | | | | (define (deep-combine combiner null-value l) | | (tree-accumulate l | | (lambda (x) x) | | combiner | | null-value)) | | | | (define (deep-map f l) | | (tree-accumulate l f cons '())) |
|
|
|
11.10.3 Mobiles
Deze oefening is gebaseerd op oefening 2.29 van
Structure
and Interpretation of Computer Programs
Een
mobile (zo’n
ding dat je aan het plafond hangt en dat met de tocht beweegt), is
ofwel een dom gewicht (getal), ofwel een koppel van twee armen, die
elk een bepaalde lengte hebben en waaraan weer een mobile hangt. Je
kan een mobile construeren door (make-mobile length1 weight1 length2 weight2), waarbij weight1 en weight2 ofwel
getallen zijn (gewichten), ofwel weer mobielen.
11.10.3.1 Constructor en selectoren
Definieer deze constructor en de selectoren (length1 mobile), (weight1 mobile), (length2 mobile), (weight2 mobile).
| (define (make-mobile length1 weight1 length2 weight2) | | (list length1 weight1 length2 weight2)) | | | | (define (length1 mobile) (list-ref mobile 0)) | | | | (define (weight1 mobile) (list-ref mobile 1)) | | | | (define (length2 mobile) (list-ref mobile 2)) | | | | (define (weight2 mobile) (list-ref mobile 3)) |
|
|
|
| > (define inner-mobile1 (make-mobile 0 2 0 4)) |
| > (define inner-mobile2 (make-mobile 0 4 0 8)) |
| > (make-mobile 1 inner-mobile1 2 inner-mobile2) |
(1 (0 2 0 4) 2 (0 4 0 8)) |
11.10.3.2 Gewicht van een mobile
Definieer (mobile-weight m), die het totaal gewicht van het
mobile teruggeeft
(het gewicht van de takken is verwaarloosbaar).
| (define (mobile-weight mobile) | | (if (atom? mobile) | | mobile | | (+ (mobile-weight (weight1 mobile)) | | (mobile-weight (weight2 mobile))))) |
|
|
|
| > (define inner-mobile1 (make-mobile 0 2 0 4)) |
| > (define inner-mobile2 (make-mobile 0 4 0 8)) |
| > (define mobile (make-mobile 1 inner-mobile1 2 inner-mobile2)) |
| > (mobile-weight mobile) |
18 |
11.10.3.3 Gebalanceerd?
Een mobile is in evenwicht wanneer het gewicht van tak 1
vermenigvuldigd met de lengte van tak 1 gelijk is aan het gewicht van
tak 2 vermenigvuldigd met de lengte van tak 2, en wanneer deze
conditie geldt voor alle sub-mobiles. Definieer het predicaat
(balanced? m), dat zegt of mobiel m gebalanceerd is.
| (define (relative-weigth1 mobile) | | (* (length1 mobile) | | (mobile-weight (weight1 mobile)))) | | | | (define (relative-weigth2 mobile) | | (* (length2 mobile) | | (mobile-weight (weight2 mobile)))) | | | | (define (balanced? mobile) | | (or (atom? mobile) | | (and (= (relative-weigth1 mobile) | | (relative-weigth2 mobile)) | | (balanced? (weight1 mobile)) | | (balanced? (weight2 mobile))))) |
|
|
|
| > (define inner-mobile1 (make-mobile 0 2 0 4)) |
| > (define inner-mobile2 (make-mobile 0 4 0 8)) |
| > (define mobile (make-mobile 1 inner-mobile1 2 inner-mobile2)) |
| > (balanced? mobile) |
#f |
| > (define inner-mobile1 (make-mobile 0 2 0 4)) |
| > (define inner-mobile2 (make-mobile 0 4 0 8)) |
| > (define mobile (make-mobile 2 inner-mobile1 1 inner-mobile2)) |
| > (balanced? mobile) |
#t |
Familiebomen & Hiërarchische Relaties
11.11 Familieboompatroon: modeloplossing
Het volgende stukje "code" beschrijft een standaardpatroon voor een familieboom.
| (define (parent tree) ...) |
| (define (children tree) ...) |
| |
| (define (tree-proc tree ...) |
| (cond ((test-parent (parent tree)) ...) |
| (else (tree-proc-in (children tree) ...)))) |
| |
| (define (tree-proc-in lst ...) |
| (cond ((null? lst) ...) |
| (else (combine-res (tree-proc (car lst) ...) |
| (tree-proc-in (cdr lst) ...))))) |
11.12 Examen Informatica 2eZit 1995
Beschouw het organigram van een bedrijf.
De meest voor de hand liggende representatie van zo’n organigram is de boomstructuur.
Hieronder vind je een voorbeeld van zo een bedrijf.
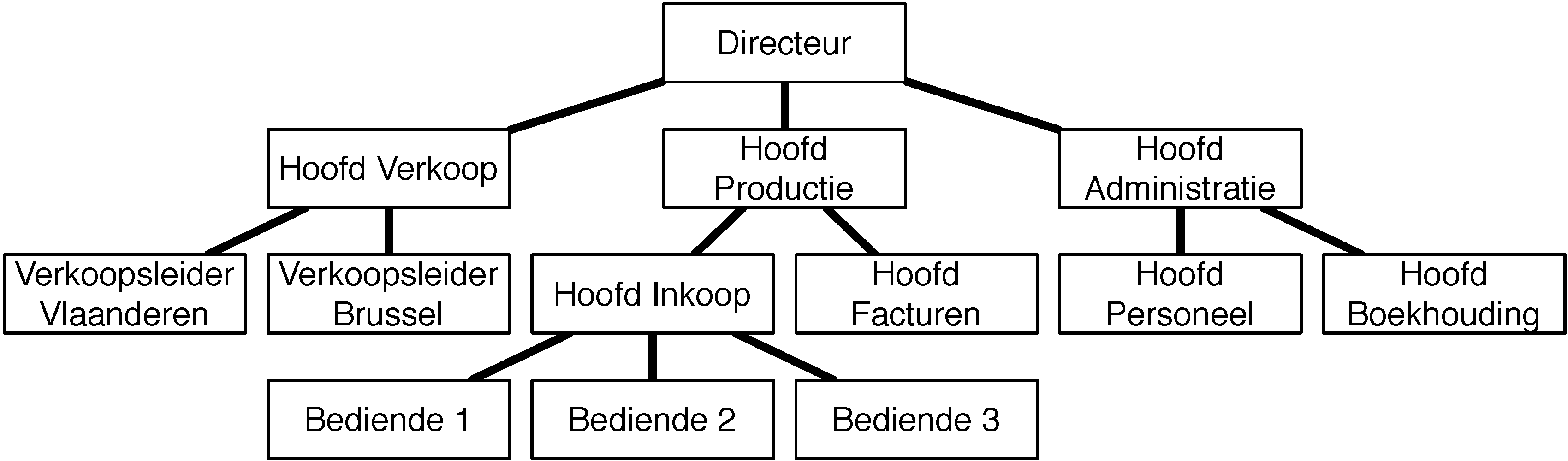
Bovenstaande boomstructuur kunnen we in Scheme gemakkelijk
voorstellen d.m.v. geneste lijsten:
| (define organigram | | '(directeur | | (hoofd-verkoop (verkoopsleider-vlaanderen) | | (verkoopsleider-brussel)) | | (hoofd-productie (hoofd-inkoop (bediende1) | | (bediende2) | | (bediende3)) | | (hoofd-fakturen)) | | (hoofd-administratie (hoofd-personeel) | | (hoofd-boekhouding)))) |
|
|
|
| > (define (baas organigram) (car organigram)) |
| > (define (sub-organigrammen organigram) (cdr organigram)) |
11.12.1 Bazen
Schrijf een procedure (bazen-van organigram p) die een lijst teruggeeft van alle bazen die in een "rechte lijn"
boven een personeelslid p staan. Met andere woorden moet je
een pad vinden van de directeur tot aan het personeelslid p.
| (define (bazen-van organigram p) | | (define (bazen-van organigram path) | | (if (eq? (baas organigram) p) | | path | | (bazen-van-in (sub-organigrammen organigram) | | (cons (baas organigram) path)))) | | (define (bazen-van-in organigrammen path) | | (if (null? organigrammen) | | #f | | (or (bazen-van (car organigrammen) path) | | (bazen-van-in (cdr organigrammen) path)))) | | (bazen-van organigram '())) |
|
|
|
| > (bazen-van organigram 'bediende2) |
(hoofd-inkoop hoofd-productie directeur) |
11.12.2 Hiërarchisch?
Schrijf een predicaat (hierarchisch? p1 p2 organigram),
dat nagaat of er een hiërarchische relatie bestaat tussen 2 personeelsleden.
(D.w.z. liggen ze op eenzelfde pad in de boom?)
| (define (hierarchisch? p1 p2 organigram) | | (define (hierarchisch?-in path organigrammen) | | (if (null? organigrammen) | | #f | | (or (hierarchisch? path (car organigrammen)) | | (hierarchisch?-in path (cdr organigrammen))))) | | | | (define (hierarchisch? path organigram) | | (cond | | ((and (eq? p1 (baas organigram)) (member p2 path)) #t) | | ((and (eq? p2 (baas organigram)) (member p1 path)) #t) | | (else (hierarchisch?-in (cons (baas organigram) path) | | (sub-organigrammen organigram))))) | | (hierarchisch? '() organigram)) |
|
|
|
| > (hierarchisch? 'directeur 'verkoopsleider-brussel organigram) |
#t |
| > (hierarchisch? 'bediende1 'hoofd-productie organigram) |
#t |
| > (hierarchisch? 'hoofd-personeel 'bediende3 organigram) |
#f |
11.12.3 Collega’s
Eén van de personeelsleden krijgt binnenkort een dochtertje.
Volgens de bedrijfstraditie moet hij daarom doopsuiker sturen naar al de
personeelsleden waarvan hij het (rechtstreekse of onrechtstreekse) hoofd is,
evenals naar al zijn oversten.
Schrijf een procedure (collegas p organigram) die een lijstje met al deze personen opstelt.
| (define (collegas p organigram) | | (define (collegas-in oversten organigrammen) | | (if (null? organigrammen) | | #f | | (or (collegas oversten (car organigrammen)) | | (collegas-in oversten (cdr organigrammen))))) | | | | (define (werknemers-in organigrammen) | | (if (null? organigrammen) | | '() | | (append (werknemers (car organigrammen)) | | (werknemers-in (cdr organigrammen))))) | | | | (define (werknemers organigram) | | (cons (baas organigram) | | (werknemers-in (sub-organigrammen organigram)))) | | | | (define (collegas oversten organigram) | | (if (eq? p (baas organigram)) | | (append oversten | | (werknemers-in (sub-organigrammen organigram))) | | (collegas-in (cons (baas organigram) oversten) | | (sub-organigrammen organigram)))) | | (collegas '() organigram)) |
|
|
|
| > (collegas 'hoofd-inkoop organigram) |
(hoofd-productie directeur bediende1 bediende2 bediende3) |
11.13 Examen Informatica januari 2010
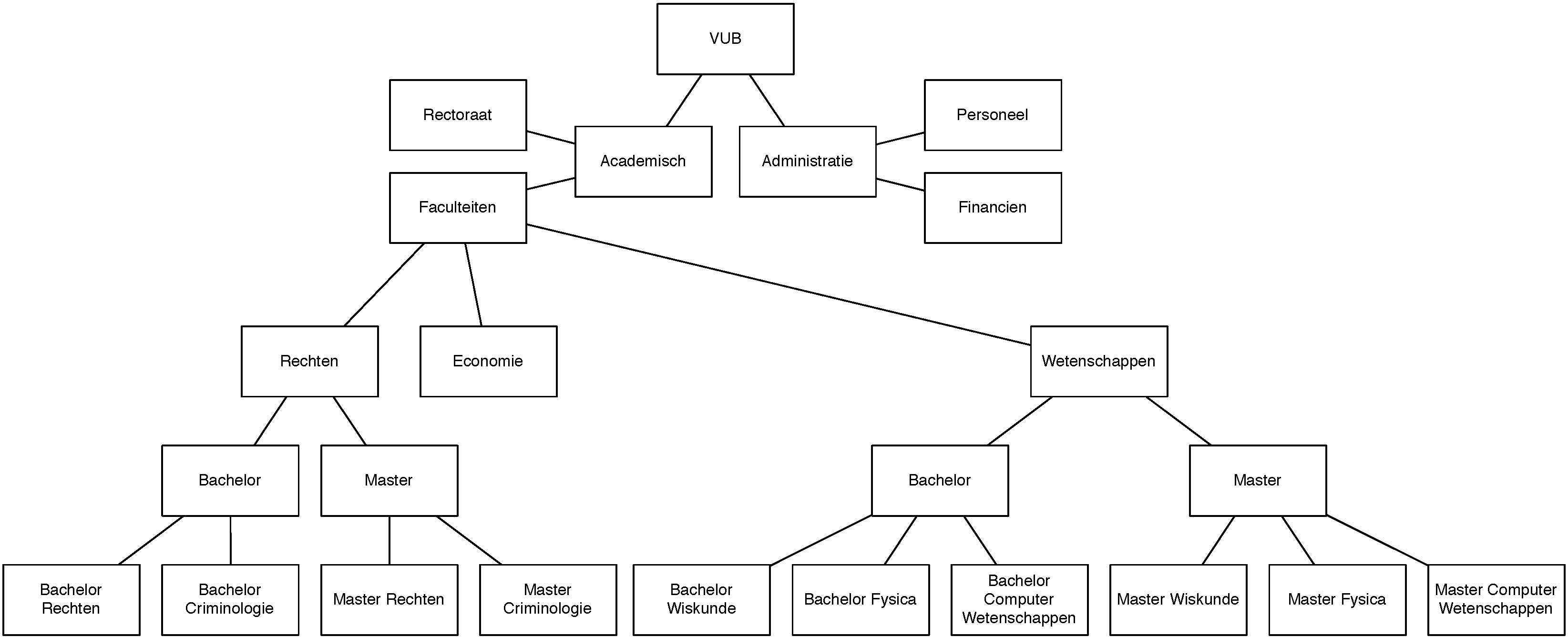
Onderstaande boomstructuur geeft een stukje weer van het organigram van de VUB.
De VUB organisatie kan onderverdeeld worden in een academisch stuk en in een
administratief stuk.
De adminstratie kan op haar beurt onderverdeeld worden in personeel, financiën, etc.
Elke dienst kan dan nog verder opgedeeld worden.
De academische organisatie bestaat uit het rectoraat en de faculteiten.
De faculteiten zijn bvb. Rechten, Economie en Wetenschappen.
(Er zijn nog andere faculteiten maar deze hebben we niet op het organigram aangeduid).
Elke faculteit heeft diverse bachelorprogramma’s en masterprogramma’s.
Let op, je oplossingen voor de vragen hieronder moeten algemeen zijn;
dus kunnen werken in situaties waar er nog een verder opdeling is van het rectoraat,
van de richtingen, etc.
| (define VUBOrganigram | | '(VUB (academisch (rectoraat) | | (faculteiten | | (rechten (bachelor (ba-rechten) | | (ba-criminologie)) | | (master (ma-rechten) | | (ma-criminologie))) | | (economie) | | (wetenschappen (bachelor (ba-wiskunde) | | (ba-fysica) | | (ba-cw)) | | (master (ma-wiskunde) | | (ma-fysica) | | (ma-cw))))) | | (administratief (personeel) (financien)))) |
|
|
|
Maw de diepte van de boom ligt niet vast.
Veronderstel dat een procedure (print-lijn aantalblanco tekst) gegeven
is die als input een getal neemt en een tekst en die de tekst afprint op 1
lijn met het gegeven aantal blanco’s ervoor.
| (define (display-n n d) | | (cond ((> n 0) (display d) | | (display-n (- n 1) d)))) | | | | (define (print-lijn aantalblanco tekst) | | (display-n aantalblanco " ") | | (display tekst) | | (newline)) |
|
|
|
| (define (label organigram) (car organigram)) | | (define (takken organigram) (cdr organigram)) |
|
|
|
11.13.1 Print-vanaf
Schrijf een procedure (print-vanaf organigram label) die
de organisatiestructuur weergeeft van een gegeven onderdeel
binnen een gegeven organigram en dit op een geïndenteerde manier.
Een voorbeeld (VUBOrganigram verwijst naar bovenstaande boomstructuur):
| (define (organigram-member-in een-label organigrammen) | | (if (null? organigrammen) | | #f | | (or (organigram-member een-label (car organigrammen)) | | (organigram-member-in een-label (cdr organigrammen))))) | | | | (define (organigram-member een-label organigram) | | (if (eq? een-label (label organigram)) | | organigram | | (organigram-member-in een-label (takken organigram)))) | | | | (define (print organigram) | | (define (print diepte organigram) | | (print-lijn diepte (label organigram)) | | (for-each (lambda (organigram) | | (print (+ diepte 1) organigram)) | | (takken organigram))) | | (print 0 organigram)) | | | | (define (print-vanaf organigram label) | | (let ((res (organigram-member label organigram))) | | (if res | | (print res) | | #f))) |
|
|
|
| > (print-vanaf VUBOrganigram 'rechten) |
rechten | bachelor | ba-rechten | ba-criminologie | master | ma-rechten | ma-criminologie |
|
11.13.2 Print-tot
Schrijf een procedure (print-tot organigram niveau) die
het organigram afprint tot op een bepaald niveau en dit terug geïndenteerd.
| (define (print-tot organigram niveau) | | (define (print organigram huidig-niveau) | | (cond ((<= huidig-niveau niveau) | | (print-lijn huidig-niveau (label organigram)) | | (print-in (takken organigram) (+ huidig-niveau 1))))) | | (define (print-in organigrammen huidig-niveau) | | (cond ((not (null? organigrammen)) | | (print (car organigrammen) huidig-niveau) | | (print-in (cdr organigrammen) huidig-niveau)))) | | (print organigram 0)) |
|
|
|
Dit kunnen we ietwat vereenvoudigen door gebruik te maken
van for-each.
| (define (print-tot organigram niveau) | | (define (print-tot organigram huidig-niveau) | | (cond ((<= huidig-niveau niveau) | | (print-lijn huidig-niveau (label organigram)) | | (for-each | | (lambda (organigram) | | (print-tot organigram (+ huidig-niveau 1))) | | (takken organigram))))) | | (print-tot organigram 0)) |
|
|
|
| > (print-tot VUBOrganigram 2) |
VUB | academisch | rectoraat | faculteiten | administratief | personeel | financien |
|
11.14 Examen Informatica januari 2008: Boom vraag
Traditiegetrouw geven (bet)(over)grootouders met Nieuwjaar nieuwjaarsgeld aan
hun nakomelingen. Veronderstel dat de nakomelingen in Scheme voorgesteld
worden als een familieboom. Bvb. beschouw de volgende familieboom, waarbij Jan
de grootouder is en nieuwjaarsgeld uitdeelt aan zijn nakomelingen. Dit kan
echter op verschillende manieren gebeuren.
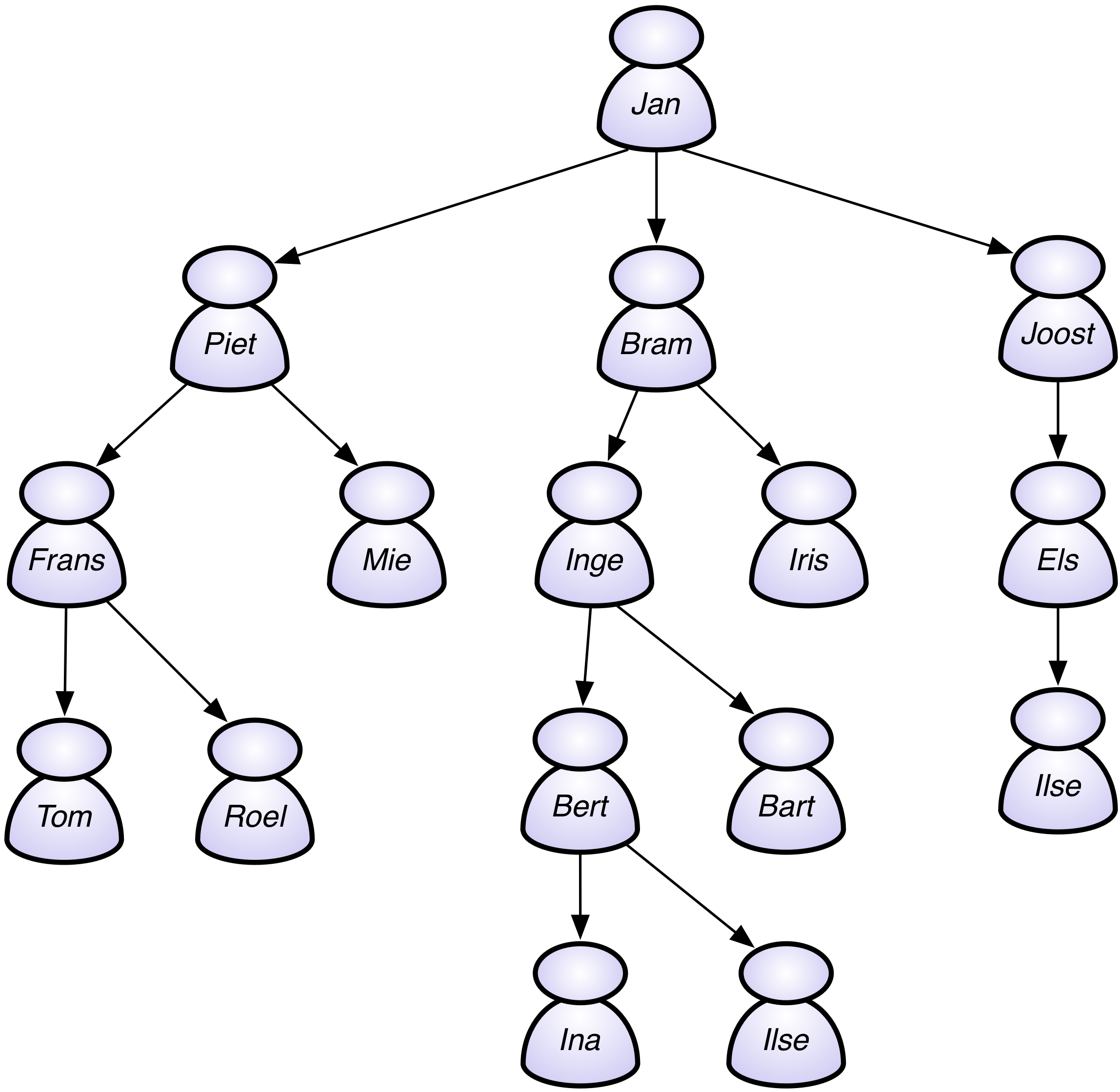
| (define familieboom '(jan (piet (frans (tom) | | (roel)) | | (mie)) | | (bram (inge (bert (ina) | | (ilse)) | | (bart)) | | (iris)) | | (joost (els (ilse))))) |
|
|
|
| (define (familiehoofd fam) (car fam)) | | (define (kinderen fam) (cdr fam)) | | (define (laatste-nakomeling? fam) | | (null? (kinderen fam))) |
|
|
|
11.14.1 Verdeel democratisch
Gegeven een budget, beslist een grootouder om iedereen evenveel geld te geven.
Schrijf een procedure verdeel-democratisch die gegeven een
familieboom en een budget, berekent hoeveel elk familielid krijgt.
| (define (verdeel-democratisch boom budget) | | (define (verdeel boom) | | (if (laatste-nakomeling? boom) | | 1 | | (+ 1 (verdeel-in (kinderen boom))))) | | | | (define (verdeel-in lst) | | (if (null? lst) | | 0 | | (+ (verdeel (car lst)) | | (verdeel-in (cdr lst))))) | | (/ budget (verdeel-in (kinderen boom)))) |
|
|
|
| > (verdeel-democratisch familieboom 1500) |
100 |
11.14.2 Bereken budget
Andere grootouders beslissen om aan hun kinderen elk 100 euro te geven, aan
hun kleinkinderen 50 euro en aan hun achterkleinkinderen 20 euro. Schrijf een
procedure budget die het budget dat de grootouders nodig hebben,
berekent.
| (define (budget boom budget-list) | | (define (budget-hulp boom budget-list) | | (if (null? budget-list) | | 0 | | (+ (car budget-list) | | (budget-hulp-in (kinderen boom) (cdr budget-list))))) | | | | (define (budget-hulp-in bomen budget-list) | | (if (null? bomen) | | 0 | | (+ (budget-hulp (car bomen) budget-list) | | (budget-hulp-in (cdr bomen) budget-list)))) | | (budget-hulp-in (kinderen boom) budget-list)) |
|
|
|
| > (budget familieboom '(100 50 20)) |
650 |
11.14.3 Verdeel budget onder nakomelingen zonder kinderen
Nog andere grootouders beslissen om enkel aan de nakomelingen die geen
kinderen hebben nieuwjaarsgeld te geven. Ze doen dit volgens het volgende
principe: hun budget wordt gelijk verdeeld over hun aantal kinderen, het
budget van elk kind wordt terug gelijk verdeeld over dat kind zijn kinderen,
enz. Schrijf een procedure verdeel die, gegeven een familieboom en
een budget, een lijstje teruggeeft waarvan elk element terug een lijstje is
met de naam van de nakomeling (die zelf geen kinderen meer heeft) en het
bedrag dat deze krijgt.
| (define (verdeel boom budget) | | (cond ((laatste-nakomeling? boom) | | (list (list (familiehoofd boom) budget))) | | (else (let* ((rest (kinderen boom)) | | (new-budget (/ budget (length rest)))) | | (verdeel-in rest new-budget))))) | | | | (define (verdeel-in bomen budget) | | (if (null? bomen) | | '() | | (append (verdeel (car bomen) budget) | | (verdeel-in (cdr bomen) budget)))) |
|
|
|
| > (verdeel familieboom 3000) |
((tom 250) | (roel 250) | (mie 500) | (ina 125) | (ilse 125) | (bart 250) | (iris 500) | (ilse 1000)) |
|
11.15 Familiebomen & Hiërarchische Relaties: Extra Oefeningen
11.15.1 Examen Informatica tweede zit 1999: Boom vraag
Naar aanleiding van het komende millenniumfeest wordt door de overheid
een steekproef gedaan naar de kwaliteit van het vuurwerk geleverd door
verschillende leveranciers. Een computermodel van een afgevuurd
vuurwerkstuk werd opgesteld in Scheme. Het ziet er als volgt uit:
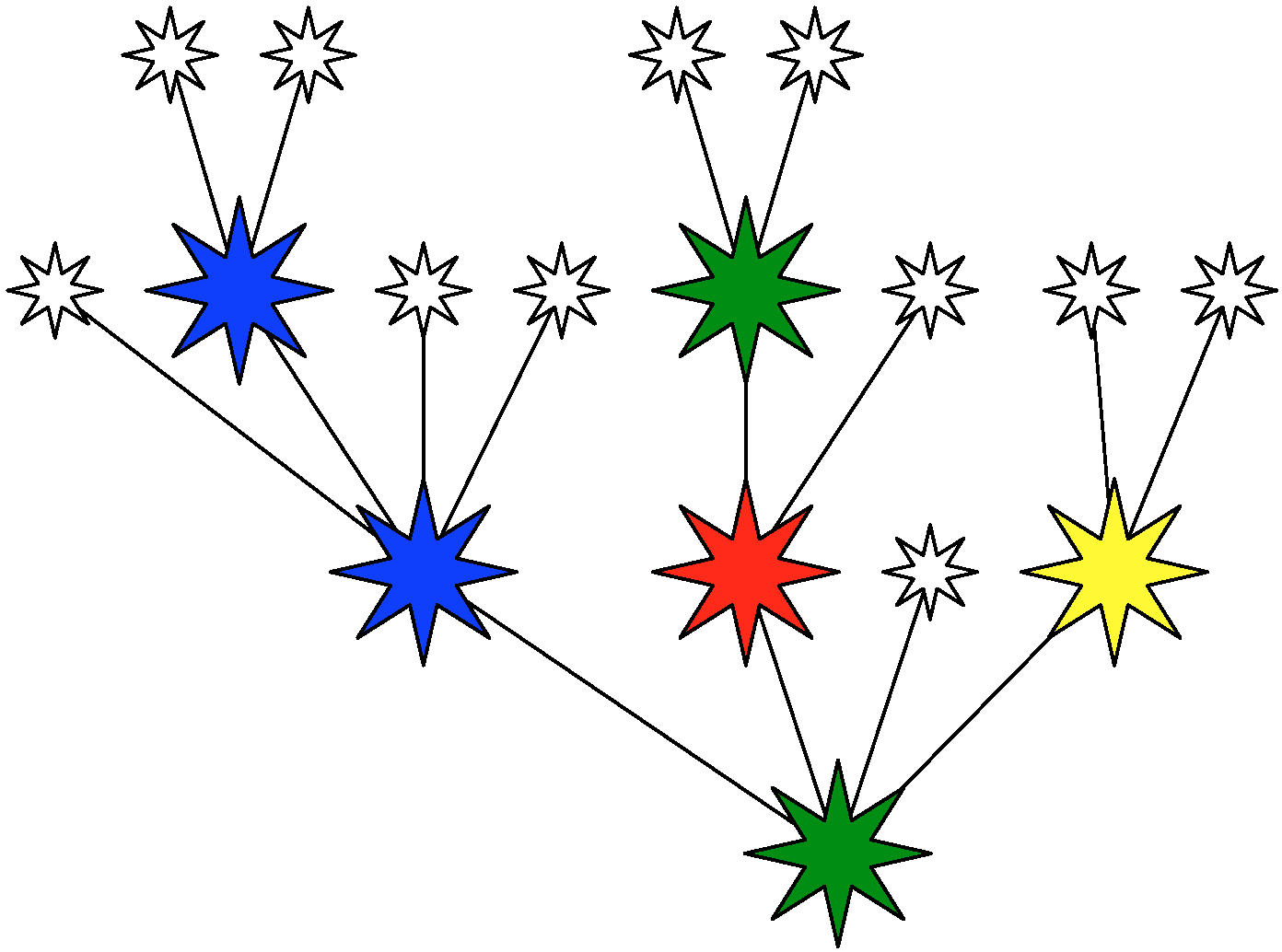
Een vuurwerk spat uit elkaar in opeenvolgende knallen. Elke knal heeft
een kleur en een aantal vertakkingen in die kleur. Een vertakking kan,
indien er nog genoeg energie is opnieuw knallen en dit eventueel in
een andere kleur. Dit geeft volgende lijstvoorstelling voor
bovenstaand voorbeeld:
| (define mijn-vuurwerk '(groen ((blauw (X (blauw (X X)) X X)) | | (rood ((groen (X X)) X)) | | X | | (geel (X X))))) |
|
|
|
Een vertakking die eindigt zonder of met te weinig energie zal niet
meer verder knallen. Dit wordt in het model aangeduid met een
'X.
We kunnen nu enkele testen implementeren:
| (define (kleur vuurwerk) (car vuurwerk)) | | (define (takken vuurwerk) (cadr vuurwerk)) | | (define (low-energy? vuurwerk) (eq? vuurwerk 'X)) |
|
|
|
| > (kleur mijn-vuurwerk) |
groen |
| > (takken mijn-vuurwerk) |
((blauw (X (blauw (X X)) X X)) (rood ((groen (X X)) X)) X (geel (X X))) |
| > (low-energy? mijn-vuurwerk) |
#f |
| > (low-energy? 'X) |
#t |
11.15.1.1 Tel-knallen
Schrijf een procedure (tel-knallen vuurwerk) die
het totaal aantal knallen van het gegeven vuurwerkstuk telt.
| (define (tel-knallen vuurwerk) | | (define (tel-knallen vuurwerk) | | (if (low-energy? vuurwerk) | | 0 | | (+ 1 (tel-knallen-in (takken vuurwerk))))) | | (define (tel-knallen-in takken) | | (if (null? takken) | | 0 | | (+ (tel-knallen (car takken)) | | (tel-knallen-in (cdr takken))))) | | (tel-knallen vuurwerk)) |
|
|
|
| > (tel-knallen mijn-vuurwerk) |
6 |
11.15.1.2 Tel-einde
Schrijf een procedure (tel-einde vuurwerk kleur) die
het aantal vertakkingen van een bepaalde kleur telt,
waarvan de energie te laag is om verder te knallen.
| (define (tel-low-energies vuurwerk) | | (define (tel vuurwerk) | | (if (low-energy? vuurwerk) | | 1 | | (tel-in (takken vuurwerk)))) | | (define (tel-in takken) | | (if (null? takken) | | 0 | | (+ (tel (car takken)) (tel-in (cdr takken))))) | | (tel vuurwerk)) | | | | (define (tel-einde vuurwerk een-kleur) | | (define (tel-einde vuurwerk) | | (cond ((low-energy? vuurwerk) 0) | | ((eq? (kleur vuurwerk) een-kleur) (tel-low-energies vuurwerk)) | | (else (tel-einde-in (takken vuurwerk))))) | | (define (tel-einde-in takken) | | (if (null? takken) | | 0 | | (+ (tel-einde (car takken)) | | (tel-einde-in (cdr takken))))) | | (tel-einde vuurwerk)) |
|
|
|
| > (tel-einde mijn-vuurwerk 'blauw) |
5 |
11.15.1.3 Ster?
Schrijf een procedure (ster? vuurwerk) die nagaat of een vuurwerkstuk
voldoet aan volgende eis: na de eerste knal heeft elke vertakking nog
voldoende energie om zelf ook te knallen. Bovendien moeten ze dit doen met elk
evenveel vertakkingen.
| (define (ster? vuurwerk) | | (define (aantal-takken vuurwerk) | | (length (takken vuurwerk))) | | (define (bekijk-takken takken prev-length) | | (cond ((null? takken) #t) | | ((low-energy? (car takken)) #f) | | ((not (= (aantal-takken (car takken)) prev-length)) #f) | | (else (bekijk-takken (cdr takken) (aantal-takken (car takken)))))) | | (if (low-energy? vuurwerk) | | #f | | (bekijk-takken (takken vuurwerk) (aantal-takken (car (takken vuurwerk)))))) |
|
|
|
| > (ster? mijn-vuurwerk) |
#f |
| > (ster? '(groen ((blauw (X X X)) | | (rood (X X X)) | | (geel (X X X)) | | (oranje (X X X)) | | (paars (X X X))))) |
|
#t |
11.15.2 Examen Informatica augustus 2009
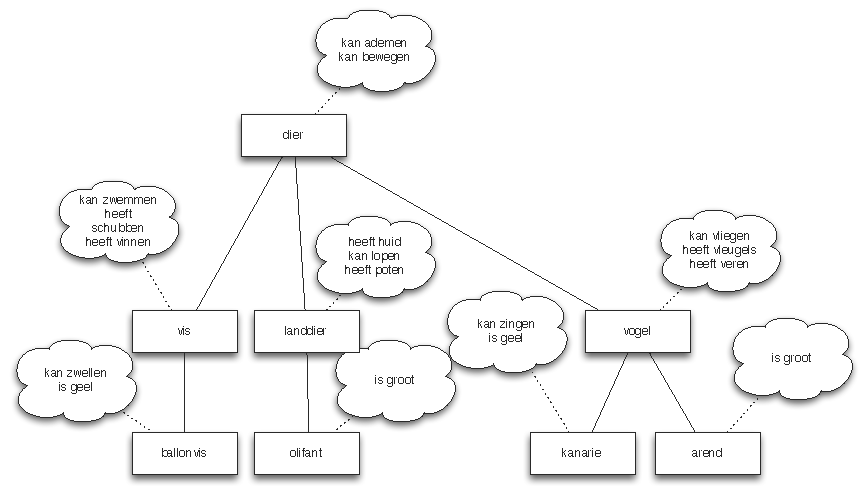
Een classificatieboom is een speciaal soort boom die een aantal soorten (van dieren, planten, ...) classificeert volgens een bepaalde hiërarchie. Elke knoop in de boom beschrijft een bepaalde soort, met zijn specifieke eigenschappen. Bijvoorbeeld een "dier" is een soort die "kan ademen" en "kan bewegen". Alle deelsoorten van een bepaalde soort hebben dezelfde eigenschappen als die soort, maar kunnen eventueel ook nog een aantal extra eigenschappen bezitten. Bijvoorbeeld een "landdier" is een speciaal geval van een "dier" dat een "huid heeft", "poten heeft" en "kan lopen", maar natuurlijk heeft het nog steeds de eigenschappen "kan ademen" en "kan bewegen", aangezien het een "dier" is.
Merk op dat we in de knopen die de deelsoorten beschrijven alleen de bijkomende eigenschappen opnemen. Hieronder vind je een uitgewerkt voorbeeld van zo’n classificatieboom:
11.15.2.1 Abstract Data Type
Implementeer het knoop ADT om een knoop van zo’n classificatieboom voor te stellen. Implementeer ook het boom ADT om de classificatieboom zelf voor te stellen.
| ADT knoop |
| |
| maak-dier |
| ( string list -> knoop ) |
| |
| naam |
| ( knoop -> string ) |
| |
| eigenschappen |
| ( knoop -> list ) |
| |
| dier? |
| ( any -> boolean ) |
| ADT boom |
| |
| maak-boom |
| ( knoop pair -> boom ) |
| |
| deelbomen |
| ( boom -> pair ) |
| |
| leeg? |
| ( boom -> boolean ) |
| |
| boom? |
| ( any -> boolean ) |
Gebruik dan de ADTs om de bovenstaande boom te maken. Noem het classificatieboom.
| "ADT voor knoop" | | (define (maak-dier naam eigenschappen) | | (list naam eigenschappen)) | | | | (define (naam dier) (car dier)) | | (define (eigenschappen dier) (cadr dier)) | | | | (define (dier? dier) | | (and (pair? dier) | | (atom? (naam dier)) | | (pair? (eigenschappen dier)))) | | | | "ADT voor boom" | | (define (maak-boom knoop deelbomen) | | (list 'knoop knoop deelbomen)) | | | | (define (knoop boom) (cadr boom)) | | (define (deelbomen boom) (caddr boom)) | | (define (leeg? boom) (null? boom)) | | (define (boom? boom) (and (pair? boom) | | (eq? (car boom) 'knoop))) | | | | | | (define classificatieboom | | (maak-boom (maak-dier 'dier '(kan-ademen kan-bewegen)) | | (list | | (maak-boom | | (maak-dier 'vis | | '(kan-zwemmen heeft-schubben heeft-vinnen)) | | (list | | (maak-boom (maak-dier 'ballonvis | | '(kan-zwellen is-geel)) | | '()))) | | (maak-boom | | (maak-dier 'landdier | | '(heeft-huid kan-lopen heeft-poten)) | | (list (maak-boom (maak-dier 'olifant | | '(is-groot)) | | '()))) | | (maak-boom | | (maak-dier 'vogel | | '(kan-vliegen heeft-vleugels heeft-veren)) | | (list | | (maak-boom (maak-dier 'kanarie | | '(kan-zingen is-geel)) | | '()) | | (maak-boom (maak-dier 'arend | | '(is-groot)) | | '())))))) |
|
|
|
11.15.2.2 Geef alle soorten
Schrijf een functie (all-kinds cboom) die een
classificatieboom cboom als invoer neemt en alle soorten uit
die classificatieboom in een lijstje teruggeeft.
| (define (all-kinds boom) | | (define (all-kinds boom) | | (cond ((leeg? boom) '()) | | (else (cons (naam (knoop boom)) | | (all-kinds-in (deelbomen boom)))))) | | (define (all-kinds-in takken) | | (if (null? takken) | | '() | | (append (all-kinds (car takken)) | | (all-kinds-in (cdr takken))))) | | (all-kinds boom)) |
|
|
|
| > (all-kinds classificatieboom) |
(dier vis ballonvis landdier olifant vogel kanarie arend) |
11.15.2.3 Verifieer eigenschap
Schrijf een predicaat (ask? cboom soort eigenschap) dat
controleert of een bepaalde soort uit de classificatieboom een bepaalde
eigenschap bezit. Hou er rekening mee dat alle eigenschappen die gelden
voor een bepaalde soort in de boom, automatisch ook gelden voor al zijn
deelsoorten, ook al staan ze daar niet expliciet opnieuw opgesomd. Zo
heeft een ballonvis bijvoorbeeld ook vinnen, aangezien alle vissen vinnen
hebben.
| (define (geef-eigenschappen boom soort) | | (define (geef-eigenschappen boom eign) | | (let ((eign (append eign (eigenschappen (knoop boom))))) | | (if (eq? (naam (knoop boom)) soort) | | eign | | (geef-eigenschappen-in (deelbomen boom) eign)))) | | (define (geef-eigenschappen-in takken eigenschappen) | | (if (null? takken) | | #f | | (or (geef-eigenschappen (car takken) eigenschappen) | | (geef-eigenschappen-in (cdr takken) eigenschappen)))) | | (geef-eigenschappen boom '())) | | | | (define (ask? boom soort eig) | | (let ((eigenschappen (geef-eigenschappen boom soort))) | | (pair? (memq eig eigenschappen)))) |
|
|
|
| > (ask? classificatieboom 'landdier 'kan-lopen) |
#t |
| > (ask? classificatieboom 'ballonvis 'heeft-vinnen) |
#t |
| > (ask? classificatieboom 'olifant 'kan-vliegen) |
#f |
11.15.3 Examen Informatica augustus 2006
Na lang onderzoek en vele experimenten zijn landbouwers erin geslaagd
om hybride fruitbomen te kweken. Onderstaand schema toont een tak uit
een hybride appel/peer boom. In dit geval kan de tak een willekeurig
aantal keer vertakken in nieuwe takken, bladeren, appelen of peren.
Het is wel zo dat in een normale hybride tak, een tak niet rechtstreeks kan vertakken in fruit van verschillende types. De rechtstreekse kinderen van een tak zijn dus in de hybride appel/peer boom ofwel appelen, blaadjes en takken; ofwel peren, blaadjes en takken. Onderstaand voorbeeld is een normale hybride tak.
11.15.3.1 Abstract Data Type
Implementeer de volgende ADTs dat toelaat om dit type boom voor te stellen en te gebruiken in Scheme.
| ADT blad |
| |
| maak-blad |
| ( any -> blad ) |
| |
| geef-type |
| ( blad -> any ) |
| |
| blad? |
| ( any -> boolean ) |
| ADT knoop |
| |
| maak-knoop |
| ( pair -> knoop ) |
| |
| geef-deelbomen |
| ( knoop -> pair ) |
| |
| knoop? |
| ( any -> boolean) |
| ADT hybride-tak |
| |
| maak-hybride-tak |
| ( pair -> hybride-tak ) |
| |
| geef-knopen |
| ( hybride-tak -> pair ) |
| |
| leeg? |
| ( hybride-tak -> boolean ) |
Gebuik dan deze operaties om de bovenstaande hybride tak voor te stellen in Scheme. Noem het hybride-tak.
| (define (maak-blad type) type) | | (define (geef-type blad) blad) | | | | (define (maak-knoop deelbomen) deelbomen) | | (define (geef-deelbomen boom) boom) | | | | (define (maak-hybride-tak knopen) knopen) | | (define (geef-knopen tak) tak) | | | | (define (leeg? boom) (null? boom)) | | (define (knoop? boom) (pair? boom)) | | (define (blad? boom) (atom? boom)) | | | | (define hybride-tak | | (maak-hybride-tak | | (list | | (maak-knoop | | (list | | (maak-knoop (list (maak-blad 'appel) | | (maak-blad 'appel) | | (maak-blad 'blad))) | | (maak-blad 'peer))) | | (maak-knoop (list (maak-blad 'blad) | | (maak-blad 'peer))) | | (maak-knoop (list (maak-blad 'appel) | | (maak-knoop (list (maak-blad 'appel) | | (maak-blad 'blad)))))))) | | | | (define tak | | (maak-hybride-tak | | (list | | (maak-knoop | | (list (maak-knoop (list (maak-blad 'appel) | | (maak-blad 'appel) | | (maak-blad 'blad))) | | (maak-blad 'peer))) | | (maak-knoop (list (maak-blad 'blad) | | (maak-blad 'peer) | | (maak-blad 'appel))) | | (maak-knoop (list (maak-blad 'appel) | | (maak-knoop (list (maak-blad 'appel) | | (maak-blad 'blad)))))))) |
|
|
|
| > hybride-tak |
(((appel appel blad) peer) (blad peer) (appel (appel blad))) |
11.15.3.2 Tel fruit en bladeren
Schrijf een functie tel die gegeven een hybride appel/peer tak, teruggeeft hoeveel appelen, peren en blaadjes aan de tak hangen.
| (define (tel boom) | | (define (combine-results l1 l2) | | (list (+ (car l1) (car l2)) | | (+ (cadr l1) (cadr l2)) | | (+ (caddr l1) (caddr l2)))) | | | | | | (define (tel-hulp boom) | | (cond ((leeg? boom) (list 0 0 0)) | | ((and (blad? boom) (eq? boom 'appel)) | | (list 1 0 0)) | | ((and (blad? boom) (eq? boom 'peer)) | | (list 0 1 0)) | | ((blad? boom) (list 0 0 1)) | | (else (tel-hulp-in (geef-knopen boom))))) | | | | (define (tel-hulp-in lst) | | (if (null? lst) | | (list 0 0 0) | | (combine-results (tel-hulp (car lst)) | | (tel-hulp-in (cdr lst))))) | | (tel-hulp boom)) |
|
|
|
| > (tel hybride-tak) |
(4 2 3) |
11.15.3.3 Normale tak?
Schrijf een functie check-normaal die nagaat of een gegeven hybride appel/peer tak normaal is, m.a.w. die nagaat of er geen knoop bestaat die zowel een appel als een peer als rechstreekse kinderen heeft.
| (define (member? x lst) | | (pair? (memq x lst))) | | | | (define (normaal? knoop) | | (let ((types (map (lambda (x) (if (pair? x) 'tak x)) knoop))) | | (not (and (member? 'appel types) (member? 'peer types))))) | | | | (define (check-normaal boom) | | (cond ((leeg? boom) #t) | | ((blad? boom) #t) | | ((knoop? boom) | | (and (normaal? boom) | | (check-normaal-in (geef-knopen boom)))) | | (else (check-normaal-in (geef-knopen boom))))) | | | | (define (check-normaal-in lst) | | (if (null? lst) | | #t | | (and (check-normaal (car lst)) | | (check-normaal-in (cdr lst))))) |
|
|
|
| > (check-normaal hybride-tak) |
#t |
11.15.4 Examen Informatica augustus 2008
Bedrijven zoals Coca-Cola, InBev, etc. hebben een uitgebreid productengamma
dat onderverdeeld is in verschillende categorieën en subcategorieën die elk
verschillende producten bevatten. Elk product haalt een bepaald omzetcijfer.
Beschouw bijvoorbeeld de volgende boom van het bedrijf Coca-Cola (die
een gelimiteerde versie van het volledige gamma voorstelt).
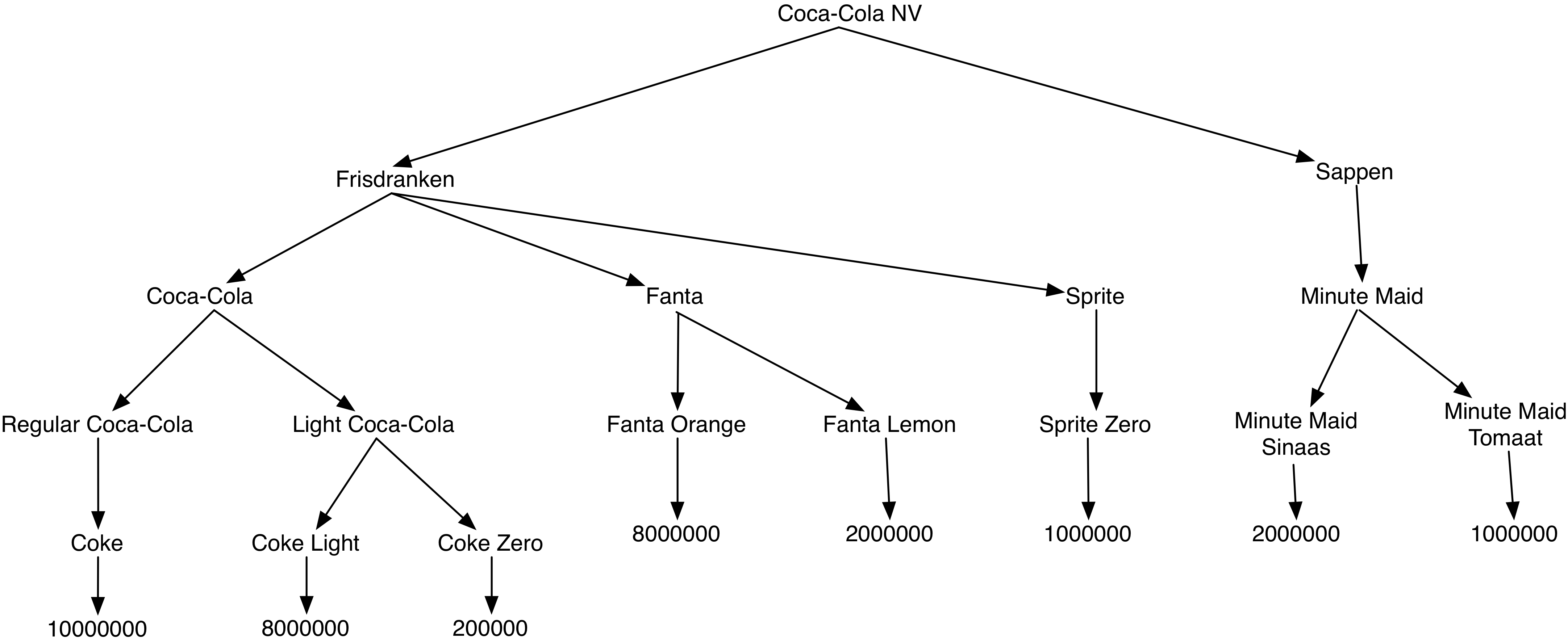
| (define Coca-Cola-NV | | '(Coca-Cola-NV (Frisdranken | | (Coca-Cola | | (Regular-Coca-Cola (Coke (10000000))) | | (light-Coca-Cola (Coke-Light (800000)) | | (Coke-Zero (200000)))) | | (Fanta (Fanta-Orange (800000)) | | (Fanta-Lemon (200000))) | | (Sprite (Sprite-Zero (1000000)))) | | (Sappen | | (Minute-Maid (Minute-Maid-Sinaas (2000000)) | | (Minute-Maid-Tomaat (1000000)))))) |
|
|
|
| (define (deel-categorien categorie) | | (cdr categorie)) | | | | (define (hoofdcategorie categorie) | | (car categorie)) |
|
|
|
11.15.4.1 Bereken omzet
Schrijf een procedure (omzet bedrijf categorie) die de totale omzet
van een gegeven categorie of product binnen het bedrijf teruggeeft.
| (define (bereken lst) | | (cond ((null? lst) 0) | | ((atom? lst) 0) | | ((number? (car lst)) (car lst)) | | (else (+ (bereken (car lst)) | | (bereken (cdr lst)))))) | | | | (define (omzet bedrijf categorie) | | (if (eq? (hoofdcategorie bedrijf) categorie) | | (bereken bedrijf) | | (omzet-in (deel-categorien bedrijf) categorie))) | | | | (define (omzet-in lst categorie) | | (if (null? lst) | | #f | | (or (omzet (car lst) categorie) | | (omzet-in (cdr lst) categorie)))) |
|
|
|
| > (omzet Coca-Cola-NV 'Coca-Cola) |
11000000 |
| > (omzet Coca-Cola-NV 'Sprite) |
1000000 |
| > (omzet Coca-Cola-NV 'Minute-Maid) |
3000000 |
11.15.4.2 Verdeel budget democratisch
De dienst marketing van zo een bedrijf heeft een bepaald budget dat op
verschillende manieren kan verdeeld worden over producten. Een eerste manier
is om het gegeven marketingbudget evenredig met het omzetcijfer te verdelen
over de producten.
Schrijf een procedure (verdeel-democratisch bedrijf budget) die een
lijstje teruggeeft met hoeveel budget elk product van het bedrijf krijgt
afhankelijk van zijn omzetcijfer.
| (define (is-product? x) | | (and (pair? x) | | (pair? (cadr x)) | | (number? (caadr x)))) | | | | (define (omzetcijfer product) | | (caadr product)) | | | | (define (producten bedrijf) | | (define (producten bedrijf) | | (if (is-product? bedrijf) | | (list (list (hoofdcategorie bedrijf) | | (omzetcijfer bedrijf))) | | (producten-in (deel-categorien bedrijf)))) | | (define (producten-in takken) | | (if (null? takken) | | '() | | (append (producten (car takken)) | | (producten-in (cdr takken))))) | | (producten bedrijf)) | | | | (define (verdeel-democratisch bedrijf budget) | | (let* ((producten (producten bedrijf)) | | (totaal (apply + (map cadr producten))) | | (factor (/ budget totaal))) | | (map (lambda (x) (list (car x) (* factor (cadr x)))) | | producten))) |
|
|
|
| > (verdeel-democratisch Coca-Cola-NV 128000000) |
((Coke 80000000) | (Coke-Light 6400000) | (Coke-Zero 1600000) | (Fanta-Orange 6400000) | (Fanta-Lemon 1600000) | (Sprite-Zero 8000000) | (Minute-Maid-Sinaas 16000000) | (Minute-Maid-Tomaat 8000000)) |
|
11.15.4.3 Onafhankelijke verdeling van het budget
Een andere strategie is om het budget per afzonderlijk product toe te kennen
onafhankelijk van het omzetzijfer van het product. Deze verdeling gebeurt dan
volgens hetvolgende principe: het algemene marketingbudget wordt gelijk
verdeeld over het aantal productcategorieën, het budget van elke categorie
wordt terug gelijk verdeeld over die categorie zijn subcategorieën, enz.
Schrijf een procedure (verdeel bedrijf budget) die gegeven een
bedrijfsboom en een budget de budgetboom teruggeeft waarbij de bladeren van de
boom niet meer het omzetcijfer bevatten, maar het marketingbudget dat elk
product volgens dit principe krijgt.
| (define (is-product? x) | | (and (pair? x) | | (pair? (cadr x)) | | (number? (caadr x)))) | | | | (define (verdeel bedrijf budget) | | (define (verdeel bedrijf budget) | | (if (is-product? bedrijf) | | (list (hoofdcategorie bedrijf) | | (list budget)) | | (let* ((rest (deel-categorien bedrijf)) | | (new-budget (/ budget (length rest)))) | | (cons (hoofdcategorie bedrijf) | | (verdeel-in rest new-budget))))) | | (define (verdeel-in takken budget) | | (if (null? takken) | | '() | | (cons (verdeel (car takken) budget) | | (verdeel-in (cdr takken) budget)))) | | (verdeel bedrijf budget)) |
|
|
|
| > (verdeel Coca-Cola-NV 1200000) |
(Coca-Cola-NV | (Frisdranken | (Coca-Cola | (Regular-Coca-Cola (Coke (100000))) | (light-Coca-Cola (Coke-Light (50000)) (Coke-Zero (50000)))) | (Fanta (Fanta-Orange (100000)) (Fanta-Lemon (100000))) | (Sprite (Sprite-Zero (200000)))) | (Sappen | (Minute-Maid (Minute-Maid-Sinaas (300000)) (Minute-Maid-Tomaat (300000))))) |
|
11.15.5 Examen Informatica januari 2005
De beginnende circusgroep "Het grote VUB-circus" oefent volop met het
bouwen van levende piramides. Een piramide kan gebouwd worden doordat
1 of meerdere artiesten een andere artiest optillen. Op zijn beurt kan
de opgetilde artiest (eventueel samen met andere opgetilde artiesten
op hetzelfde niveau) een andere artiest optillen. Omwille van de
veiligheid kan een artiest slechts 1 artiest optillen. Onrechtstreeks
steunt hij echter alle artiesten die rechtstreeks en onrechtstreeks
ondersteund worden door de artiest die hij zelf mee optilt. We kunnen
deze piramides voorstellen door bomen, zoals bijvoorbeeld in
onderstaande figuur. De kinderen van een knoop zijn al de artiesten
die de artiest in de gegeven knoop optillen.
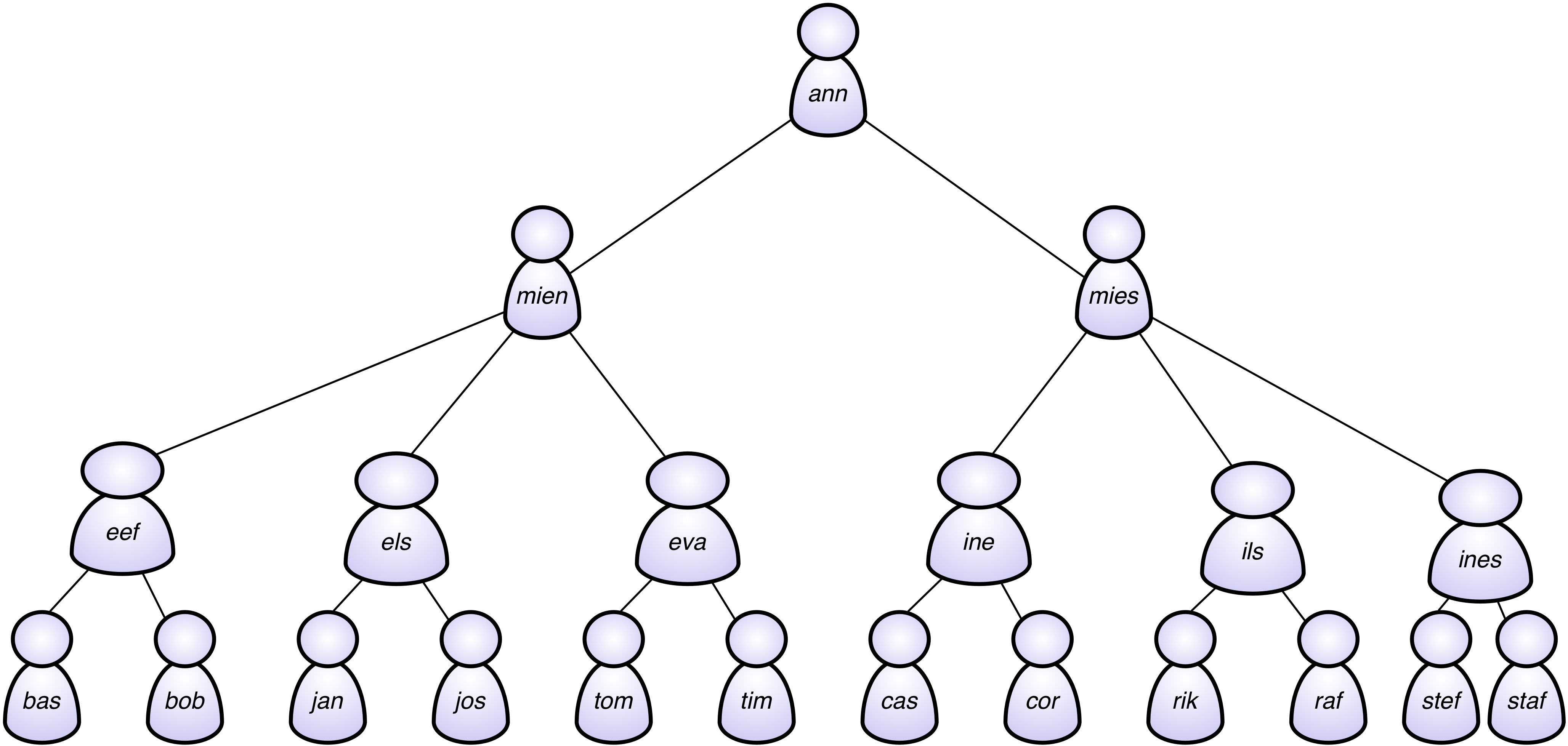
We kunnen deze piramides in Scheme voor stellen door geneste
lijsten. De geneste lijst representatie voor deze specifieke piramide
is de volgende:
| (define VUB-circus '(ann (mien (eef (bas) | | (bob)) | | (els (jan) | | (jos)) | | (eva (tom) | | (tim))) | | (mies (ine (cas) | | (cor)) | | (ils (rik) | | (raf)) | | (ines (stef) | | (staf))))) |
|
|
|
| (define (hoofdartiest piramide) (car piramide)) | | (define (artiesten piramide) (cdr piramide)) | | (define (artiest? piramide) | | (and (pair? piramide) (atom? (car piramide)))) | | (define (onderaan? piramide) (null? (cdr piramide))) |
|
|
|
Gegeven deze representatie, schrijf de volgende piramide bewerkingen
op in Scheme:
11.15.5.1 Laat ondersteunde artiesten springen
Simuleer het feit dat een artiest zijn last niet meer kan dragen:
Wanneer een artiest het te moeilijk krijft om zijn last te dragen,
roept hij alle artiesten die hij rechtstreeks en onrechtstreeks steunt
dat ze eraf moeten springen. Zelf doet hij dit niet. Met andere
woorden, de artiest die hijzelf mee optilt moet springen alsook degene
die door deze laatste mee wordt opgetild, enz.
Schrijf een Scheme functie jump, die een piramide en de naam
van de artiest die roept als input neemt en die de namen van de
artiesten die hierbij moeten springen teruggeeft in een lijstje.
| (define (jump piramide artiest) | | (define (jump-hulp piramide pad) | | (if (and (artiest? piramide) | | (eq? (hoofdartiest piramide) artiest)) | | pad | | (jump-in (artiesten piramide) | | (cons (hoofdartiest piramide) pad)))) | | | | (define (jump-in lst pad) | | (if (null? lst) | | #f | | (or (jump-hulp (car lst) pad) | | (jump-in (cdr lst) pad)))) | | (reverse (jump-hulp piramide '()))) |
|
|
|
| > (jump VUB-circus 'eva) |
(ann mien) |
| > (jump VUB-circus 'stef) |
(ann mies ines) |
11.15.5.2 Laat een artiest uit de piramide vallen
Simuleer een val van een artiest: wanneer een artiest zodanig uit
evenwicht geraakt dat hij uit de piramide valt, zullen ook al de
artiesten die hij rechtstreeks en onrechtstreeks ondersteunt
meevallen, alsook alle artiesten die hem rechtstreeks dragen (dus alle
artiesten van 1 niveau lager die hem rechtstreeks optillen, en niet
degene daaronder).
Schrijf een procedure fall, die een piramide en de naam van
de artiest die valt als input neemt, en die de namen van alle
artiesten die vallen teruggeeft in een lijstje.
| (define (fall piramide artiest) | | (define (fall-hulp piramide pad) | | (if (and (artiest? piramide) | | (eq? (hoofdartiest piramide) artiest)) | | (append pad | | (list (hoofdartiest piramide)) | | (map hoofdartiest (artiesten piramide))) | | (fall-in (artiesten piramide) | | (cons (hoofdartiest piramide) pad)))) | | | | (define (fall-in lst pad) | | (if (null? lst) | | #f | | (or (fall-hulp (car lst) pad) | | (fall-in (cdr lst) pad)))) | | (fall-hulp piramide '())) |
|
|
|
| > (fall VUB-circus 'eva) |
(mien ann eva tom tim) |
| > (fall VUB-circus 'stef) |
(ines mies ann stef) |
| > (fall VUB-circus 'mies) |
(ann mies ine ils ines) |


 Geen resultaat; oneindige lus
Geen resultaat; oneindige lus






