9 Closures en Omgevingsdiagrammen
9.1 sum & add-c
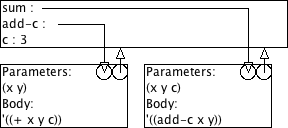
9.1.1 Omgevingsmodel-diagram
Teken het omgevingsmodel-diagram voor de volgende definities:
(define c 3) (define (add-c x y) (+ x y c)) (define (sum x y c) (add-c x y))
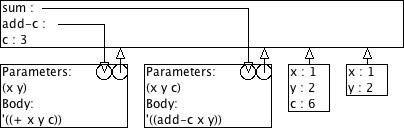
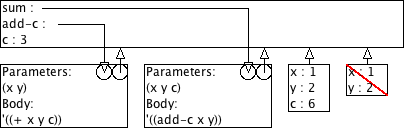
9.1.2 Voorspel het resultaat van "sum"
Voorspel het resultaat van volgende expressie aan de hand van omgevingsmodel-diagrammen.
> (sum 1 2 6) 6
9.2 Omgevingsmodellen voor let-expressies
9.2.1 Lambda
Leg uit wat er mis gaat bij de evaluatie van de volgende expressie. Hint: Zet de let om in de overeenkomstige lambda expressie en teken dan het omgevingsmodel-diagram.
(let ((x 1) (y (+ 1 x))) (+ x y))
> ((lambda (x y) (+ x y)) 1 (+ 1 x)) +: contract violation
expected: number?
given: (mcons (mcons (mcons 'c (mcons 'd '())) '()) (mcons
(mcons 'c (mcons 'd '())) '()))
argument position: 2nd
other arguments...:
1
9.2.2 Omgevingsmodel-diagrammen
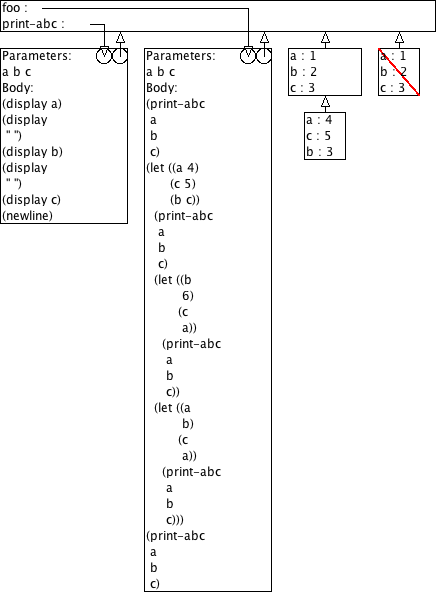
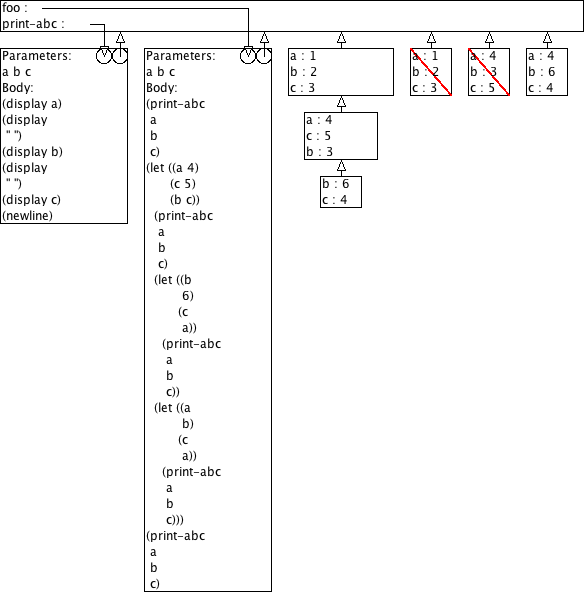
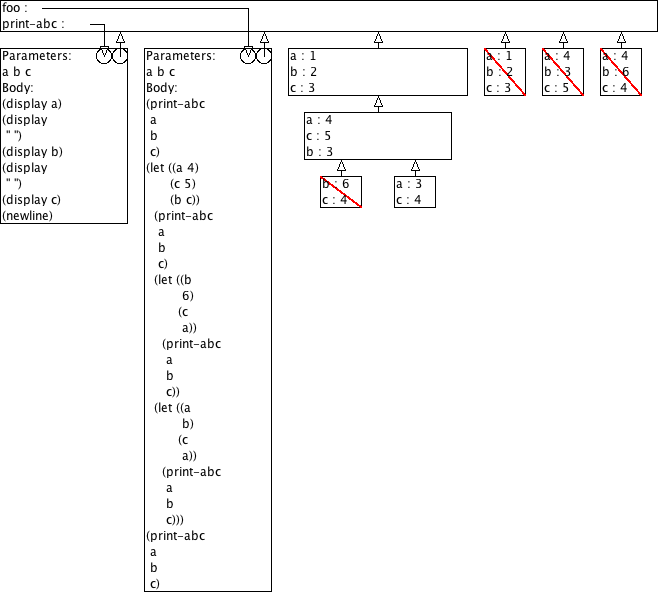
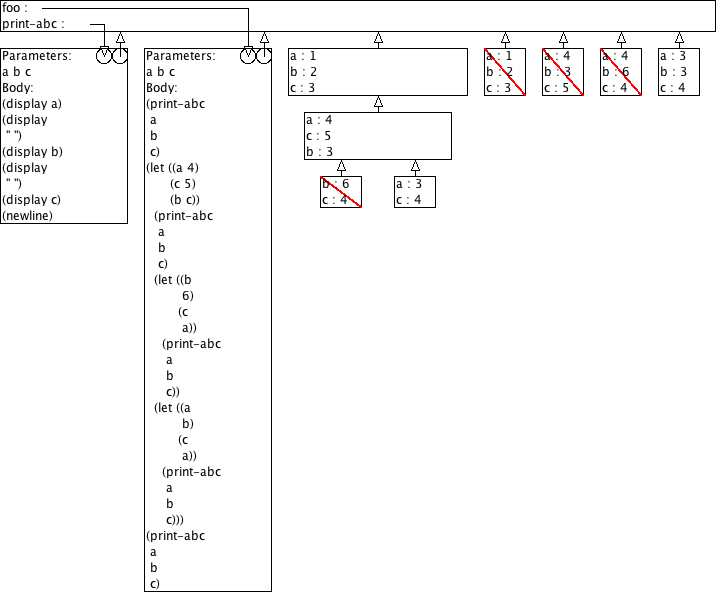
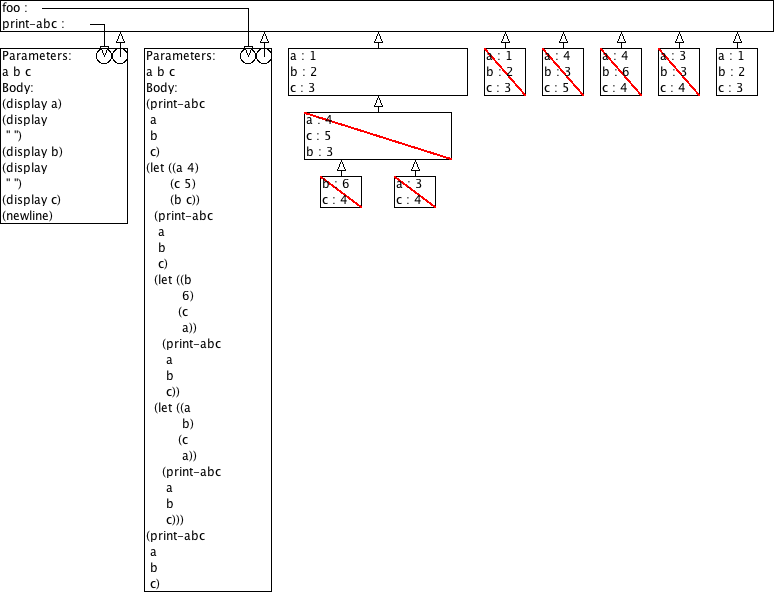
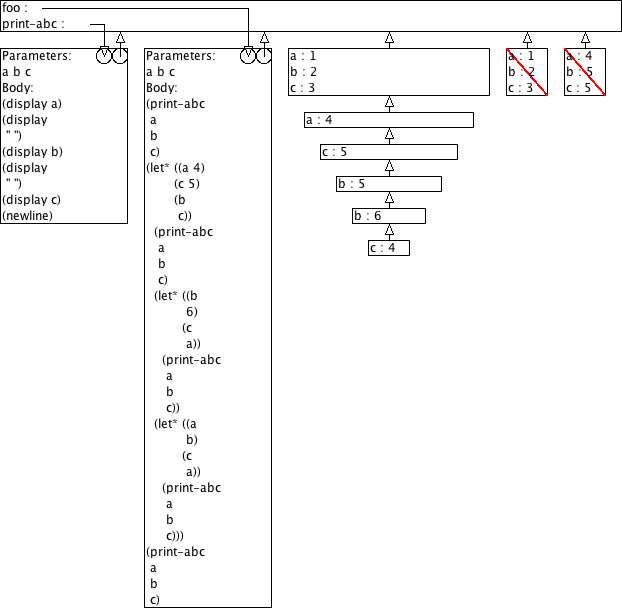
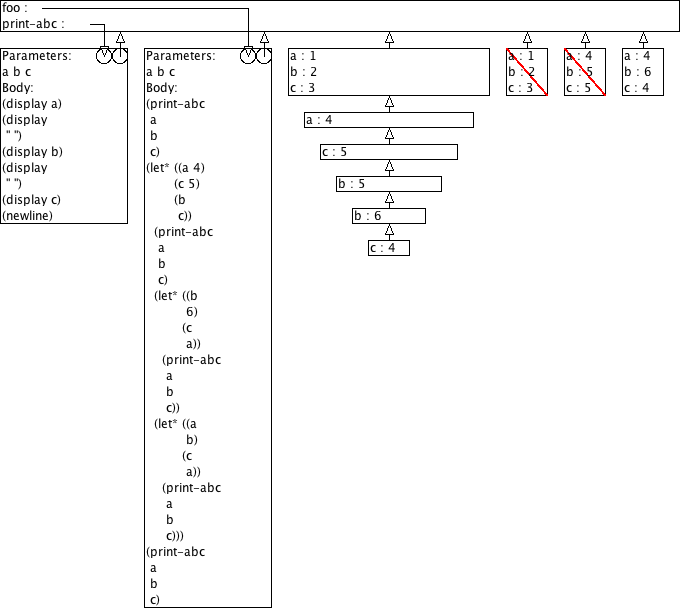
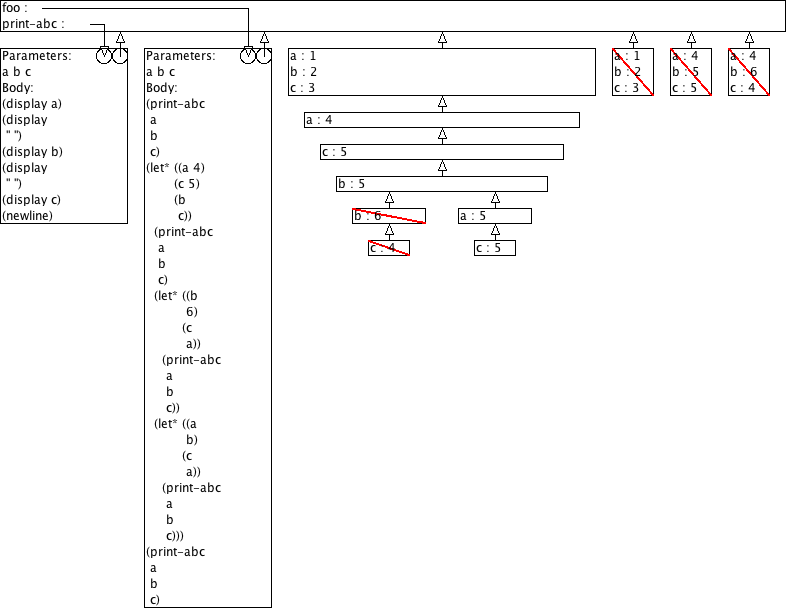
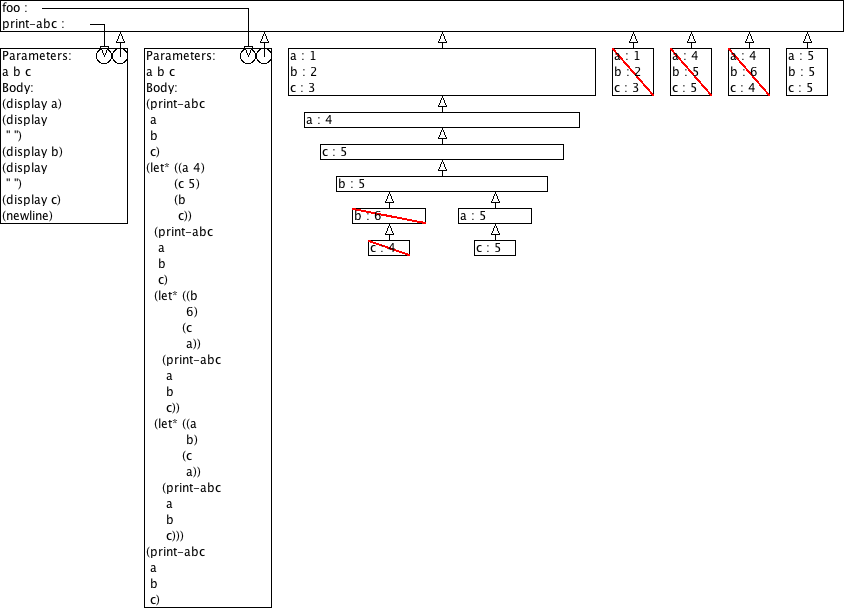
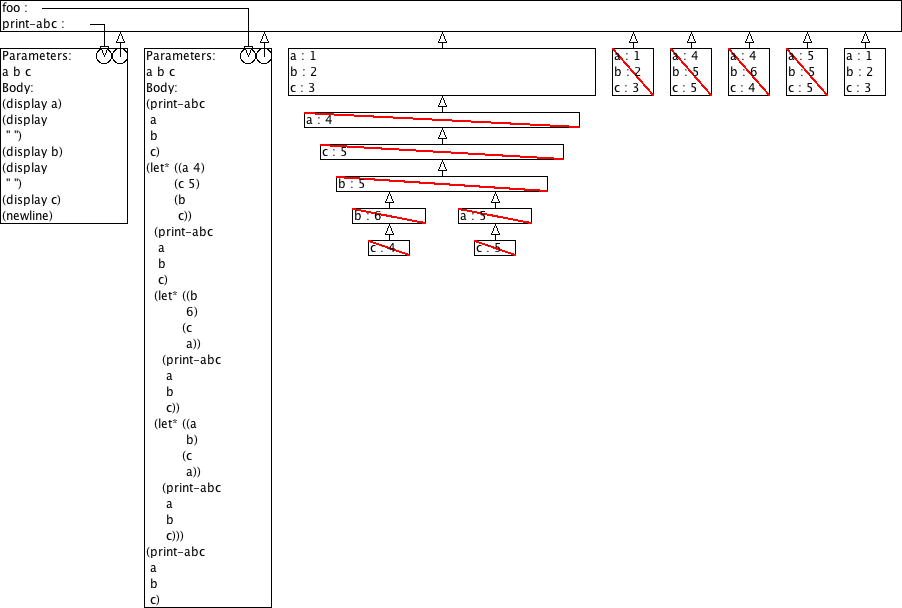
Voorspel de output van (foo 1 2 3) aan de hand van omgevingsmodel-diagrammen.
(define (print-abc a b c) (display a) (display " ") (display b) (display " ") (display c) (newline)) (define (foo a b c) (print-abc a b c) (let ((a 4) (c 5) (b c)) (print-abc a b c) (let ((b 6) (c a)) (print-abc a b c)) (let ((a b) (c a)) (print-abc a b c))) (print-abc a b c))
> (foo 1 2 3)
1 2 3
4 3 5
4 6 4
3 3 4
1 2 3
9.3 Omgevingsmodellen voor let*-expressies
9.3.1 Lambda
Zet de let* om in de overeenkomstige lambda expressie. Leg uit, met behulp van een omgevingsmodel-diagram, waarom er deze keer niets misgaat.
(let* ((x 1) (y (+ 1 x))) (+ x y))
((lambda (x) ((lambda (y) (+ x y))(+ 1 x))) 1)
9.3.2 Omgevingsmodel-diagrammen voor "print-abc"
Voorspel de output van (foo 1 2 3) aan de hand van omgevingsmodel-diagrammen.
(define (print-abc a b c) (display a) (display " ") (display b) (display " ") (display c) (newline)) (define (foo a b c) (print-abc a b c) (let* ((a 4) (c 5) (b c)) (print-abc a b c) (let* ((b 6) (c a)) (print-abc a b c)) (let* ((a b) (c a)) (print-abc a b c))) (print-abc a b c))
> (foo 1 2 3)
1 2 3
4 5 5
4 6 4
5 5 5
1 2 3
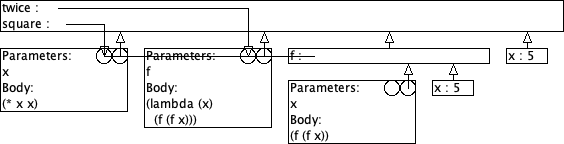
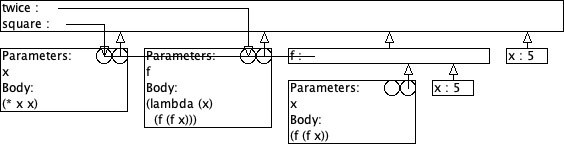
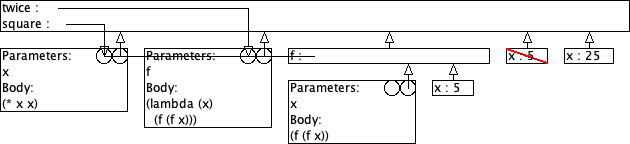
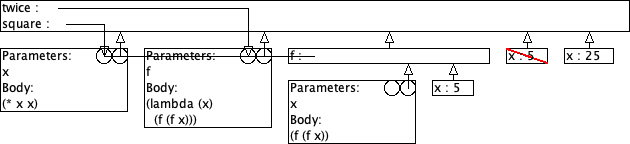
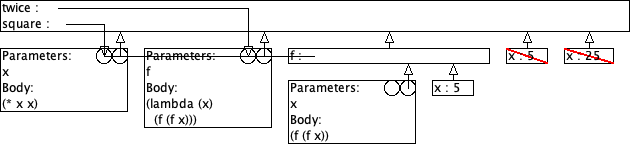
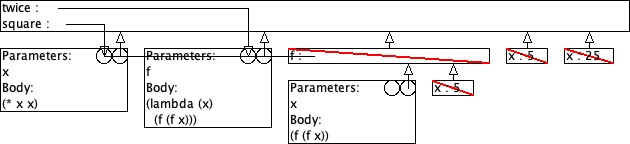
9.4 Twice: omgevingsmodel-diagram
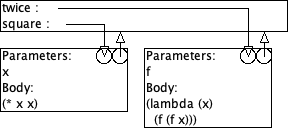
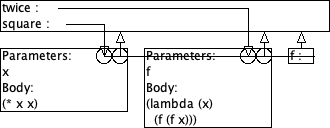
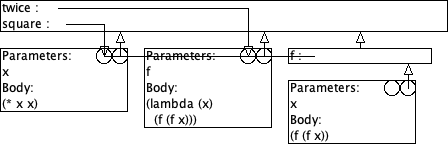
Gegeven zijn volgende definities:
(define (square x) (* x x)) (define (twice f) (lambda (x) (f (f x))))
> ((twice square) 5) 625
9.5 Examen Informatica Partieel januari 1995
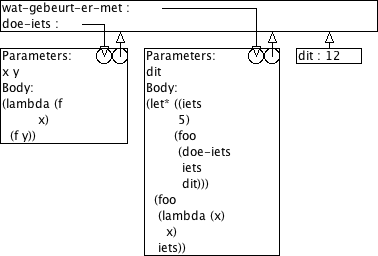
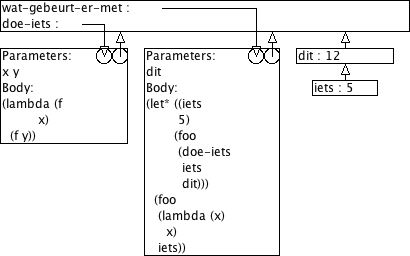
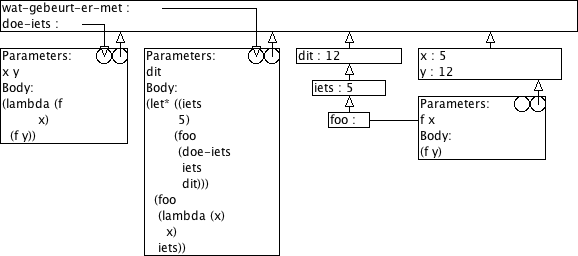
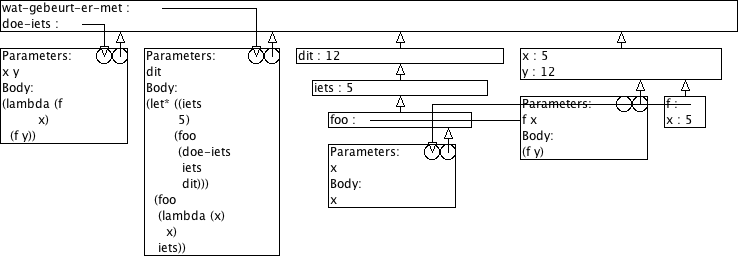
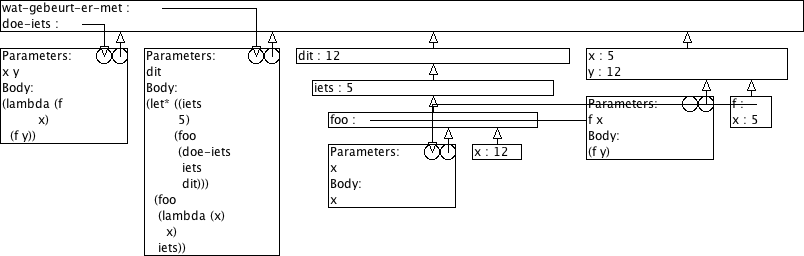
(define (doe-iets x y) (lambda (f x) (f y))) (define (wat-gebeurt-er-met dit) (let* ((iets 5) (foo (doe-iets iets dit))) (foo (lambda (x) x) iets)))
Wat is dan het resultaat van de volgende procedure-aanroepen? (Wat doet de procedure wat-gebeurt-er-met dus eigenlijk?) Verklaar je antwoord aan de hand van omgevingsmodel-diagrammen.
> (wat-gebeurt-er-met 12) 12
> (wat-gebeurt-er-met 9) 9
9.6 sum & add-c: Dynamische Scoping
Beschouw de volgende definities uit sum & add-c:
(define c 3) (define (add-c x y) (+ x y c)) (define (sum x y c) (add-c x y))
Wat zou het resultaat van (sum 1 2 6) geweest zijn indien Scheme een taal was met dynamische, in tegenstelling tot statische scoping (ook wel gekend als lexicale scoping)?
> (+ 1 2 6) 9
9.7 Dynamische Scoping: Voorspel
Deze oefening is gebaseerd op de "Lexicale Scoping vs. Dynamische Scoping" slide uit hoofdstuk 3.
Gegeven zijn volgende definities:
(define var 'global) (define (proc1) (display var)) (define (proc2) (define var 'local) (proc1))
Voorspel het resultaat van volgende expressies indien Scheme een taal was met dynamische scoping:
1. (proc1)
'global
2. (proc2)
'local
9.8 Interne staat
9.8.1 Flip
Definieer een procedure (flip) die 1 teruggeeft bij de eerste oproep, 0 bij de tweede oproep, 1 bij de derde oproep, enzovoort.
(define flip (let ((state 0)) (lambda () (if (= state 0) (set! state 1) (set! state 0)) state)))
> (flip) 1
> (flip) 0
> (flip) 1
> (flip) 0
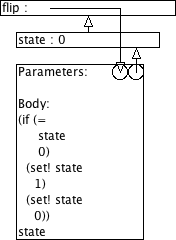
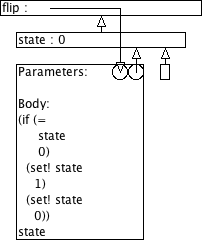
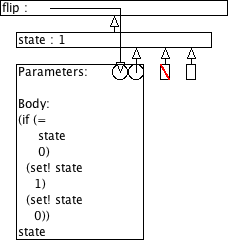
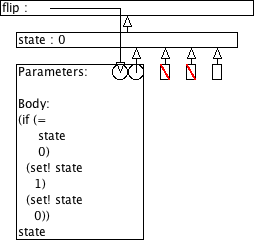
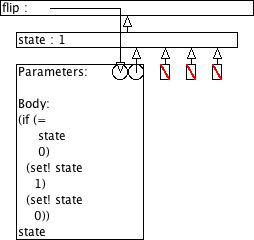
9.8.2 Omgevingsmodel-diagram voor flip
Gebruik het omgevingsmodel om elke oproep van flip uit Flip te analyseren.
9.8.3 Make-flip
Schrijf een procedure (make-flip) die kan gebruikt worden om de procedure flip als volgt te definiëren: (define flip (make-flip)).
(define (make-flip) (let ((state 0)) (lambda () (if (= state 0) (set! state 1) (set! state 0)) state)))
9.8.4 Voorspel
(define flip (make-flip)) (define flap1 (flip)) (define (flap2) (flip)) (define flap3 flip) (define (flap4) flip)
Wat is dan de waarde van de volgende expressies (indien ze in deze volgorde worden geëvalueerd)?
> flap1 1
> flap2 #<procedure:flap2>
> flap3 #<procedure>
> flap4 #<procedure:flap4>
> (flap1) application: not a procedure;
expected a procedure that can be applied to arguments
given: 1
arguments...: [none]
> (flap2) 0
> (flap3) 1
> (flap4) #<procedure>
> flap1 1
> (flap3) 0
> (flap2) 1
9.9 Extra Oefeningen
9.9.1 Pairs als procedures
Deze oefening is gebaseerd op oefening 2.4 van Structure and Interpretation of Computer Programs
Het is mogelijk om pairs, net zoals getallen en andere vormen van data, voor te stellen als procedures:
(define (my-cons x y) (lambda (m) (m x y))) (define (my-car z) (z (lambda (p q) p)))
> (my-car (my-cons 1 2)) 1
9.9.1.1 Definitie van my-cdr
Vervolledig de definities van hierboven door my-cdr te implementeren.
(define (my-cdr z) (z (lambda (p q) q)))
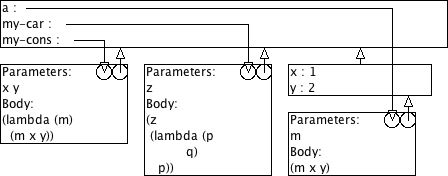
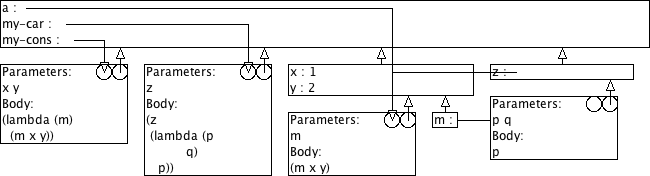
9.9.1.2 Omgevingsmodel voor my-cons
Teken een omgevingsmodel-diagram voor evaluatie van de volgende expressies.
(define a (my-cons 1 2)) (my-car a) (my-cdr a)
9.9.2 Examen Informatica Partieel januari 1994
Boudewijn moet een programma schrijven waarin hij dikwijls elk element van een volledige lijst moet ophogen met een bepaald getal. Boudewijn herinnert zich de map-over-list uit de cursus en schrijft nog een functie add-n die n toevoegt bij een gegeven getal.
(define (map-over-list a-list a-function) (cond ((null? a-list) '()) (else (cons (a-function (car a-list)) (map-over-list (cdr a-list) a-function))))) (define add-n (lambda (x) (+ x n)))
Boudewijn is een voorzichtig baasje en probeert het geheel eens uit zoals hieronder. Hij is tevreden, het werkt.
> (define n 2) > (map-over-list '(1 2 3 4 5) add-n) (3 4 5 6 7)
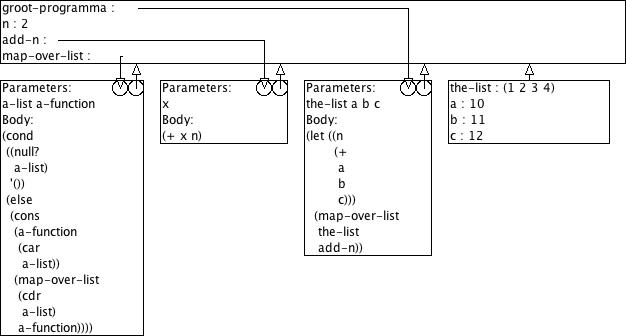
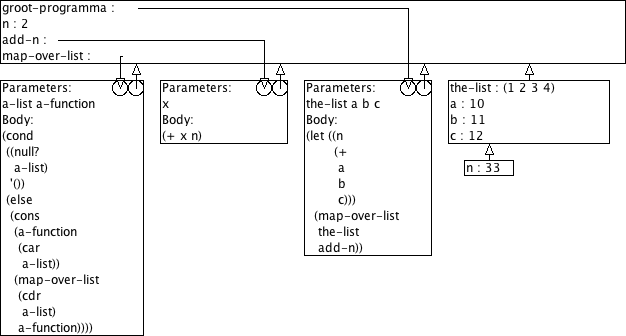
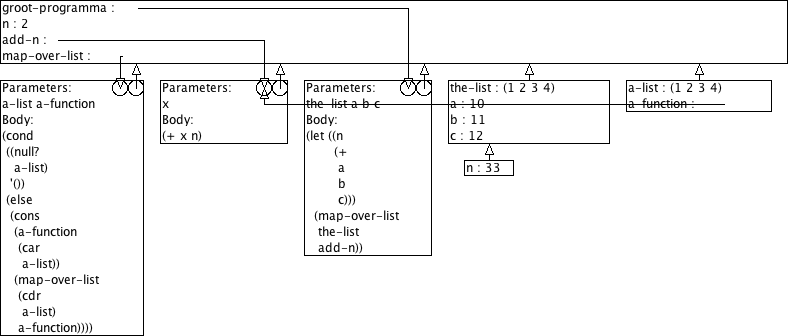
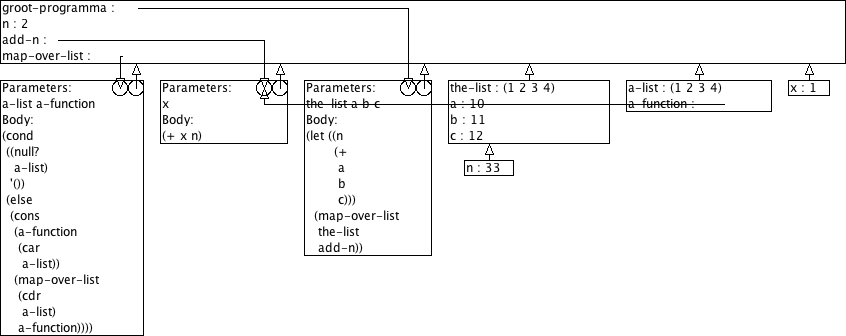
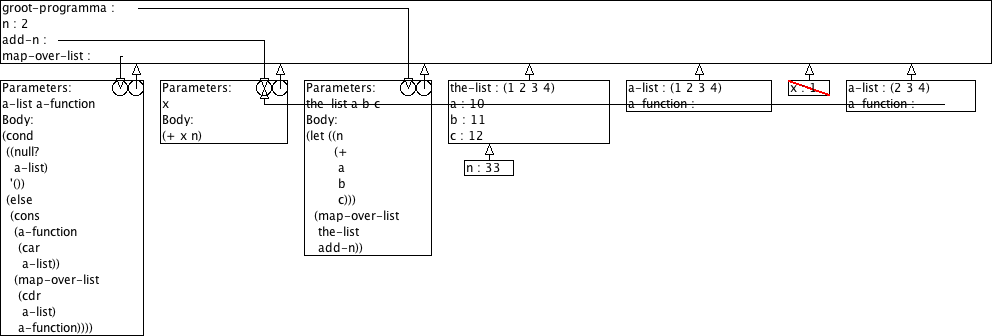
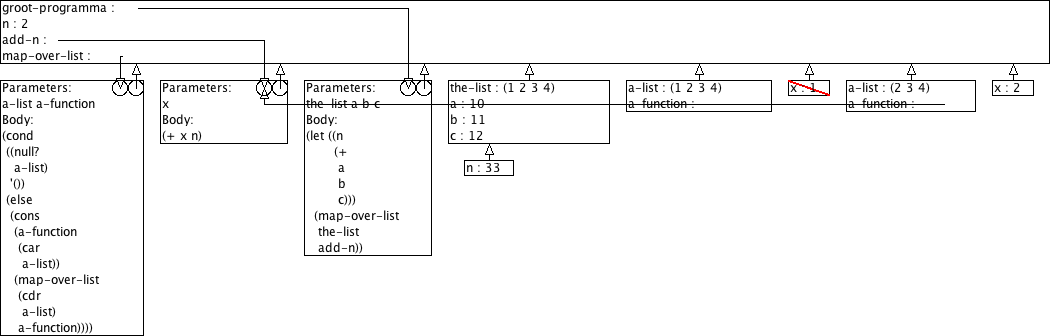
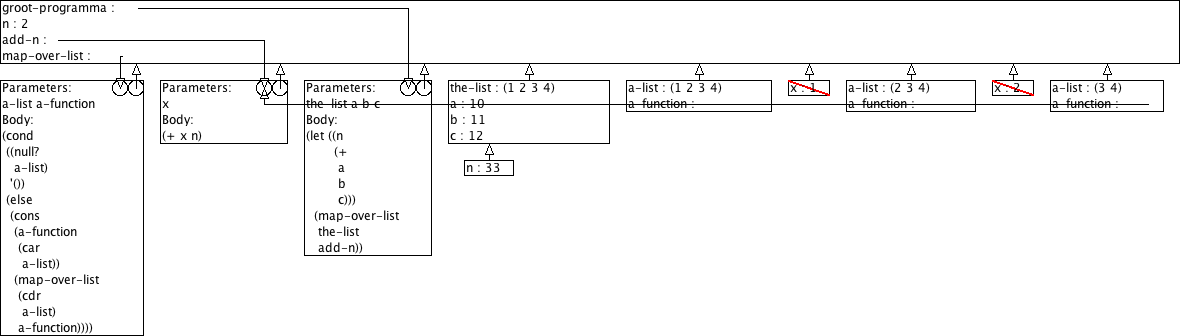
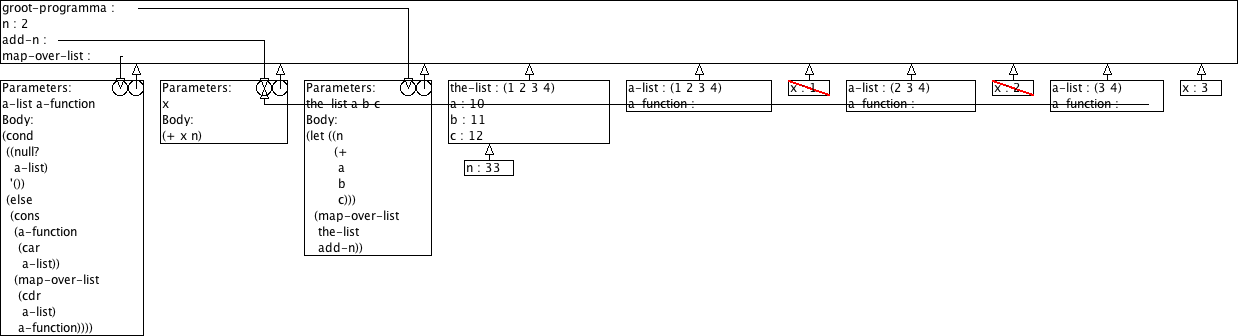
Boudewijn verwerkt dit nu in zijn groot programma zoals hieronder geschetst. Hij is niet tevreden, het werkt niet.
(define (groot-programma the-list a b c) (let ((n (+ a b c))) (map-over-list the-list add-n)))
Na lang zoeken en prutsen komt Boudewijn tot de vaststelling dat het stukje programma dat elk element van een lijst zou moeten ophogen met n het blijkbaar niet doet. Om het even welke getallen die hij bij de oproep van zijn programma voor a, b, en c gebruikt, de lijstelementen worden altijd opgehoogd met 2.
Leg jij eens uit wat er verkeerd loopt. Gebruik daarvoor het omgevingsmodel voor evaluatie. Wij verwachten hier dus een aantal tekeningen plus wat begeleidende tekst.