6 Hogere Orde Procedures

6.1 product

Deze oefening is gebaseerd op oefening 1.31 van Structure and Interpretation of Computer Programs

Beschouw de hogere-orde procedure sum uit Abelson and Sussman blz.58.

(define (sum term a next b)   (if (> a b)       0       (+ (term a) (sum term (next a) next b))))

6.1.1 Constructieve recursie

Definieer de procedure (product factor a next b), naar analogie met de hogere-orde procedure sum uit vorige oefening. Maak hierbij gebruik van constructieve recursie.

(define (product factor a next b)   (if (> a b)       1       (* (factor a) (product factor (next a) next b))))

6.1.2 Staartrecursie

Schrijf de vorige procedure nu ook op iteratieve wijze. Noem deze versie (iter-product factor a next b).

(define (iter-product factor a next b)   (define (iter a res)     (if (> a b)         res         (iter (next a) (* (factor a) res))))   (iter a 1))

6.1.3 factorial

Schrijf factorial met behulp van product.

(define (factorial n)   (define (incr x) (+ x 1))   (define (id x) x)   (product id 1 incr n))

6.2 product en sum met accumulate

Deze oefening is gebaseerd op oefening 1.32 van Structure and Interpretation of Computer Programs

6.2.1 accumulate

Schrijf de procedure (accumulate combiner null-value term a next b), die een veralgemening is van de procedures sum en product. Schrijf accumulate op iteratieve wijze. combiner is een procedure die specificeert hoe de huidige term moet ‘ gecombineerd worden met de accumulatie van de voorgaande termen. null-value specificeert de initiëele waarde van de accumulatie.

(define (accumulate combiner null-value term a next b)   (define (iter a res)     (if (> a b)         res         (iter (next a) (combiner (term a) res))))   (iter a null-value))

6.2.2 product en sum

Schrijf product en sum met behulp van accumulate.

(define (sum term a next b)   (accumulate + 0 term a next b))   (define (product factor a next b)   (accumulate * 1 factor a next b))

6.2.3 add en multiply

Schrijf de procedures (add a b) en (multiply a b) om respectievelijk 2 positieve getallen op te tellen en te vermenigvuldigen. Maak hierbij gebruik van accumulate.

Tip: kijk naar oefeningen 3.1 en 3.2 voor inspiratie.

6.3 Accumuleren met een filter

Deze oefening is gebaseerd op oefening 1.33 van Structure and Interpretation of Computer Programs

6.3.1 filtered-accumulate

Veralgemeen de procedure accumulate naar de procedure (filtered-accumulate combiner filter? null-value term a next b). Deze procedure heeft een extra argument filter?, een predikaat dat bepaalt welke termen er geaccumuleerd worden en welk niet. Zorg ervoor dat je procedure een iteratief process genereert.

(define (filtered-accumulate combiner filter? null-value term a next b)   (define (iter a res)     (if (> a b)         res         (iter (next a)               (if (filter? a)                   (combiner (term a) res)                   res))))   (iter a null-value))

6.3.2 Grootste gemene deler

Schrijf een procedure (product-gcd n) die het product berekent van alle gehele getallen \(i < n\) waarvoor geldt dat (= (gcd i n) 1). (Opmerking: gcd is een voorgedefinieerde Scheme-procedure die de grootste gemene deler van 2 getallen berekent.)

(define (product-gcd n)   (define (incr x) (+ x 1))   (define (id x) x)   (define (filter? a)     (= (gcd a n) 1))   (filtered-accumulate * filter? 1 id 1 incr n))

> (product-gcd 6)

5

> (product-gcd 7)

720

6.4 Syntactische Suiker: define met lambda-notatie

Geef voor elk van de volgende expressies een definitie van f zodanig dat de expressie de waarde 5 teruggeeft. Zorg ervoor dat elke definitie de vorm (define f <uitdrukking>) aanneemt.

1. (define f 5)

   > f

   5

2. (define f (lambda () 5))

   > (f)

   5

3. (define f (lambda (x) 5))

   > (f 3)

   5

4. (define f (lambda () (lambda () 5)))

   > ((f))

   5

5. (define f (lambda () (lambda () (lambda (drie) 5))))

   > (((f)) 3)

   5

6.5 Het verschil tussen let en let*

6.5.1 Atoma-schriftjes

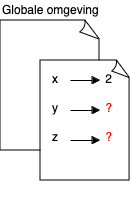
Teken voor onderstaande expressies het bijhorende omgevingsmodel met behulp van de Atoma-schriftjes metafoor.

Verklaar - indien van toepassing - wat er misgaat bij het evalueren van een expressie aan de hand van de Atoma-schift.

(let ((x 2)

(y (+ x 8))

(z (/ y x)))

(+ x y z))

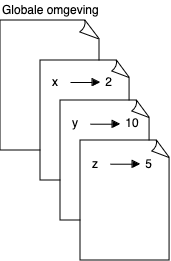
(let* ((x 2)

(y (+ x 8))

(z (/ y x)))

(+ x y z))

6.5.2 Lambda-notatie

Vorm onderstaande expressies om naar hun overeenkomstige lambda-notatie.

Verklaar - indien van toepassing - wat er misgaat bij het evalueren van een expressie aan de hand van de overeenkomstige lambda-expressie.

(let ((x 2)

(y (+ x 8))

(z (/ y x)))

(+ x y z))

((lambda (x y z)

(+ x y z))

2 (+ x 8) (/ y x))

(let* ((x 2)

(y (+ x 8))

(z (/ y x)))

(+ x y z))

((lambda (x)

((lambda (y)

((lambda (z)

(+ x y z))

(/ y x)))

(+ x 8)))

2)

6.6 compose

Schrijf een algemene procedure compose, die twee procedures f en g van 1 enkele parameter x als invoer neemt, en als uitvoer de samengestelde functie \(f \circ g\) teruggeeft.

(define (compose f g)   (lambda (x) (f (g x))))

> (define (f x) (* x x))

> (define (g x) (+ x 2))

> (f (g 3))

25

> (compose f g)

#<procedure>

> ((compose f g) 3)

25

6.7 Procedures die procedures maken

6.7.1 do-n

Schrijf een procedure (do-n f n) die een parameterloze procedure en een getal n als invoer krijgt, en deze procedure n keer uitvoert.

(define (print-hallo)   (display "hallo")   (newline))

(define (do-n f n)   (if (> n 0)       (begin         (f)         (do-n f (- n 1)))))

> (do-n print-hallo 2)

hallo hallo

6.7.2 make-do-n

Schrijf een procedure (make-do-n f n) die een parameterloze procedure (bv. print-hallo) als invoer krijgt, en als resultaat een parameterloze procedure teruggeeft die bij aanroep hetzelfde doet als de ingevoerde parameterloze procedure, maar dan n keer.

Maak gebruik van een do-lus om make-do-n te implementeren.

(define (make-do-n f n)   (lambda ()     (do ((i 1 (+ i 1)))       ((> i n))       (f))))

> (make-do-n print-hallo 2)

#<procedure>

> ((make-do-n print-hallo 2))

hallo hallo

6.7.3 Verband

Wat is het verband tussen do-n en make-do-n? Schrijf make-do-n2, die equivalent is aan make-do-n, maar die gebruikt maakt van do-n.

(define (make-do-n2 f n)   (lambda () (do-n f n)))

> (make-do-n2 print-hallo 2)

#<procedure>

> ((make-do-n2 print-hallo 2))

hallo hallo

6.8 Hogere Orde Procedures op lijsten

6.8.1 replace d.m.v. map

Implementeer de procedure replace-dmv-map, door middel van de ingebouwde procedure map. De replace-dmv-map-procedure geeft een lijst terug die gelijk is aan lijst l, maar waarin alle elementen gelijk aan e1 vervangen zijn door e2. Gebruik (eq? e1 e2) om twee elementen te vergelijken.

(define (replace-dmv-map e1 e2 l)   (map (lambda (x) (if (eq? x e1) e2 x)) l))

> (replace-dmv-map 1 999 '(1 2 1 3 1 4 1 5 1))
(999 2 999 3 999 4 999 5 999)
> (replace-dmv-map 1 999 '(2 3 4 5 6 7))
(2 3 4 5 6 7)
> (replace-dmv-map 1 999 '(1))
(999)
> (replace-dmv-map 1 999 '())
()

6.8.2 all?

Implementeer de procedure (all? pred l), die een predicaat pred en een lijst l als argumenten neemt. De procedure geeft een boolean terug die aangeeft of elk element in de lijst aan het predicaat voldoet.

(define (all? pred l)   (cond ((null? l) #t)         ((pred (car l))          (all? pred (cdr l)))         (else #f)))

> (all? even? '(2 4 6 8))

#t

> (all? even? '(2 3 4 5))

#f

6.8.3 zip

Implementeer de procedure (zip lst1 lst2 combine) die twee lijsten en een combinator als argumenten neemt, en een lijst teruggeeft die bestaat uit elementen die de paarsgewijze combinatie zijn van de overeenkomstige elementen uit de twee lijsten. Je mag ervan uitgaan dat de twee lijsten evenveel elementen bevatten.

(define (zip lst1 lst2 combine)   (if (null? lst1)       '()       (cons (combine (car lst1) (car lst2))             (zip (cdr lst1) (cdr lst2) combine))))

> (zip '(1 2 3 4) '(5 6 7 8) +)

(6 8 10 12)

> (zip '(1 2 3 4) '(5 6 7 8) -)

(-4 -4 -4 -4)

6.8.4 sum-of-squares d.m.v. zip

Implementeer een procedure (sum-of-squares lst1 lst2) die twee lijsten als argumenten neemt, en een lijst teruggeeft waarvan elk element de som van de kwadraten is van de overeenkomstige elementen uit de twee lijsten. Gebruik hiervoor de zip-procedure uit de vorige oefening.

(define (sum-of-squares lst1 lst2)   (define (square x) (* x x))   (zip lst1 lst2 (lambda (a b) (+ (square a) (square b)))))

> (sum-of-squares '(1 2 3 4) '(5 6 7 8))

(26 40 58 80)

6.9 Extra Oefeningen

6.9.1 De Regel van Simpson

Deze oefening is gebaseerd op oefening 1.29 van Structure and Interpretation of Computer Programs

Schrijf de procedure (simp-int f a b n) die de integraal van een functie f tussen a en b benadert d.m.v. de regel van Simpson: \(\frac{h}{3}\left( y_0 + 4y_1 + 2y_2 + 4y_3 + 2y_4 + \dots + 2y_{n-2} + 4y_{n-1} + y_n \right)\) met \(h = \frac{b-a}{n}\), en \(y_k = f(a + kh)\).

(define (incr x) (+ x 1))

> (define (simp-int f a b n)     (let ((h (/ (- b a) n)))       (define (y k) (f (+ a (* h k))))       (define (term k)         (* (if (or (= k 0)(= k n)) 1 (+ 2 (* 2 (modulo k 2))))            (y k)))       (/ (* h (sum term 0 incr n)) 3)))

> (simp-int (lambda (x) x) 0 10 100)

50

> (define r (sqrt 2))

> (simp-int (lambda (x) (sqrt (- (* r r) (* x x)))) (- r) r 100)

3.1402925778303366

Hint: Maak gebruik van de hogere-orde procedure sum:

(define (sum term a next b)   (if (> a b)       0       (+ (term a) (sum term (next a) next b))))

6.9.2 Lokaal maximum

Definieer met behulp van accumulate (zie oefening accumulate) een procedure (max-interval f a b) die een benadering geeft van de maximum waarde van een functie f over het interval \(\left[a, b\right]\).

Het is slechts een benadering omdat een interval eigenlijk oneindig veel (zelfs overaftelbaar veel) elementen bevat. Maak gebruik van de voorgedefinieerde Scheme-procedure max.

(define (max-interval f a b)   (define (incr i) (+ i 1))   (accumulate max (f a) f a incr b))

6.9.3 Reeksontwikkeling

Definieer (calc-e n), (calc-sin x n) en (calc-cos x n) (zie oefeningenreeks 3) met behulp van accumulate. Weeg aan de hand van deze oefening de voor- en nadelen af van het gebruik van hogere orde functies zoals accumulate.

(define (factorial n)   (if (zero? n)       1       (* n (factorial (- n 1)))))   (define (calc-e n)   (define (term i) (/ 1 (factorial i)))   (define (incr i) (+ i 1))   (accumulate + 0 term 0 incr n))   (define (calc-sin x n)   (define (incr x) (+ x 1))   (define (term i)     ((if (= (modulo i 2)0) - +)      (let ((i (+ (* 2 i) 1)))        (/ (expt x i) (factorial i)))))   (accumulate + 0 term 0 incr n))   (define (calc-cos x n)   (define (incr x) (+ x 1))   (define (term i)     ((if (= (modulo i 2)0) + -)      (let ((i (* 2 i)))        (/ (expt x i) (factorial i)))))   (accumulate + 0 term 0 incr n))

6.9.4 Vierkantsvergelijkingen

Schrijf een procedure (make-vkv a b c), die als parameters de coëfficienten a, b en c van een vierkantsvergelijking van de vorm \(ax^2+bx+c\) heeft en de vierkantsvergelijking als functie van één enkele parameter x teruggeeft.

(define (make-vkv a b c)   (lambda (x)     (+ (* a x x)        (* b x)        c)))

Definieer daarna een vierkantsvergelijking \(vkv(x)=3x^2+5x+1\) m.b.v. de functie make-vkv, en teken het omgevingsmodel-diagram voor de oproep (vkv 3.14).

> (define vkv (make-vkv 3 5 1))

> (vkv 3.14)

46.278800000000004

6.9.5 repeated

Definieer een procedure (repeated f n) die een procedure teruggeeft die f \(n\) maal toepast, m.a.w. een procedure die (f (f ... (f x))) berekent. Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (repeated f n) en de iteratieve versie (iter-repeated f n).

(define (repeated f n)   (lambda (x)     (if (= n 0)         x         (f ((repeated f (- n 1)) x)))))   (define (iter-repeated f n)   (lambda (x)     (define (iter i res)       (if (< i n)           (iter (+ i 1) (f res))           res))     (iter 0 x)))

> (repeated (lambda (x) (+ x 1)) 3)

#<procedure>

> ((repeated (lambda (x) (+ x 1)) 3) 0)

3

> (iter-repeated (lambda (x) (+ x 1)) 3)

#<procedure>

> ((iter-repeated (lambda (x) (+ x 1)) 3) 0)

3

6.9.6 combine-special

Definieer een functie (combine-special f1 f2 comb), die van de twee eerste procedures een nieuwe procedure maakt door ze te combineren met comb. Voorbeeld: (combine-special sin cos +) levert de procedure (lambda (x) (+ (sin x) (cos x))) op.

(define (combine-special f1 f2 comb)   (lambda (x)     (comb (f1 x) (f2 x))))

Definieer d.m.v. combine-special de functie \(\frac{2x + 2(\sin{x} \times \cos{x})}{x}\). Noem deze functie f in Scheme (die 1 argument verwacht).

(define any-value (lambda (x) 'any-value)) (define id (lambda (x) x)) (define double (lambda (x) (* x 2))) (define double-left (lambda (a b) (* a 2))) (define f (combine-special            (combine-special             double             (combine-special               (combine-special sin cos *)               any-value               double-left)             +)            id            /))

> (f 3.86)

2.256745564653961