2 Eenvoudige Procedures

7.8

2 Eenvoudige Procedures

2.1 Prefixnotatie

2.1.1 Van infix- naar prefixnotatie

Schrijf op een blad papier de volgende expressies in Scheme-notatie (prefixnotatie). Indenteer om de leesbaarheid te verhogen. Je kan je oplossing ook direct ingeven in DrRacket.

$\frac{a + b}{e} - \frac{c + d}{f}$
(- (/ (+ a b)
      e)
   (/ (+ c d)
      f))
$c + \frac{a}{b \times c + \frac{d}{e + \frac{f}{g}}}$
(+ c
   (/ a
      (+ (* b c)
         (/ d
            (+ e
               (/ f g))))))
$\frac{a+\frac{b}{c}}{d} \times \frac{e}{\frac{g}{i}-h}$
(* (/ (+ a
         (/ b c))
      d)
   (/ e
      (- (/ g i)
         h)))

2.2 Voorspel het resultaat van eenvoudige expressies

Voorspel (zonder gebruik te maken van een Scheme vertolker) voor elk van onderstaande expressies het resultaat indien ze in de gegeven volgorde geëvalueerd worden. Leg de gevallen uit waarbij het misloopt.

Controleer nadien, door middel van een Scheme vertolker, of je prognoses correct was. Probeer de fouten die je gemaakt hebt te begrijpen en uit te leggen.

> (* (+ 2 2) 5)
20
> (* (+ 2 2) (5))
application: not a procedure;
expected a procedure that can be applied to arguments
given: 5
arguments...: [none]
> (*(+(2 2) 5))
application: not a procedure;
expected a procedure that can be applied to arguments
  given: 2
  arguments...:
   2
> (*(+ 22)5)
110
> (5 * 4)
application: not a procedure;
expected a procedure that can be applied to arguments
  given: 5
  arguments...:
   #<procedure:*>
   4
> 5*4
5*4: undefined;
cannot reference an identifier before its definition
in module: 'program
> (define 5*4 20)
> 5*4
20
> (5 * 2+2)
2+2: undefined;
cannot reference an identifier before its definition
in module: 'program
> (* 5 (2+2))
2+2: undefined;
cannot reference an identifier before its definition
in module: 'program
> (* 5 (2 + 2))
application: not a procedure;
expected a procedure that can be applied to arguments
  given: 2
  arguments...:
   #<procedure:+>
   2
> (5*2 + 2)
5*2: undefined;
cannot reference an identifier before its definition
in module: 'program
> (5*4 + 2)
application: not a procedure;
expected a procedure that can be applied to arguments
  given: 20
  arguments...:
   #<procedure:+>
   2
> (5* (+ 2 2))
5*: undefined;
cannot reference an identifier before its definition
in module: 'program
> ((+ 2 3))
application: not a procedure;
expected a procedure that can be applied to arguments
given: 5
arguments...: [none]
> (/ 6 2)
3
> /
#<procedure:/>

2.3 Voorspel het resultaat van eenvoudige expressies a.d.h.v. omgevingsmodellen

Voorspel (zonder gebruik te maken van een Scheme vertolker) voor elk van onderstaande expressies het resultaat indien ze in de gegeven volgorde geëvalueerd worden.

Maak gebruik van omgevingsmodellen (m.b.v. de metafoor met Atoma-shriftjes) om de resultaten te bespreken, en leg de gevallen uit waarbij het misloopt. Controleer nadien, door middel van een Scheme vertolker, of je prognoses correct waren. Probeer de fouten die je gemaakt hebt te begrijpen en uit te leggen.

> (define $ /)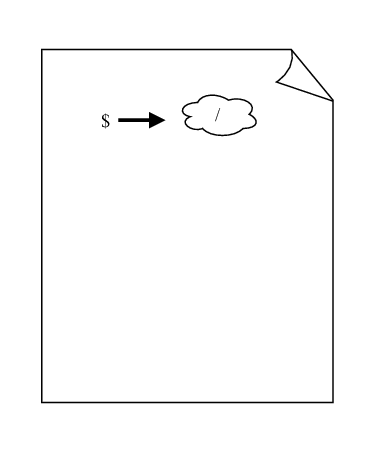
> ($ 6 2)
3
> $
#<procedure:/>
> (define (double x) (+ x x))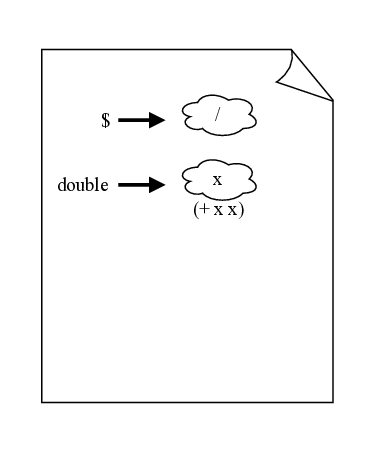
> (double (double 5))
20
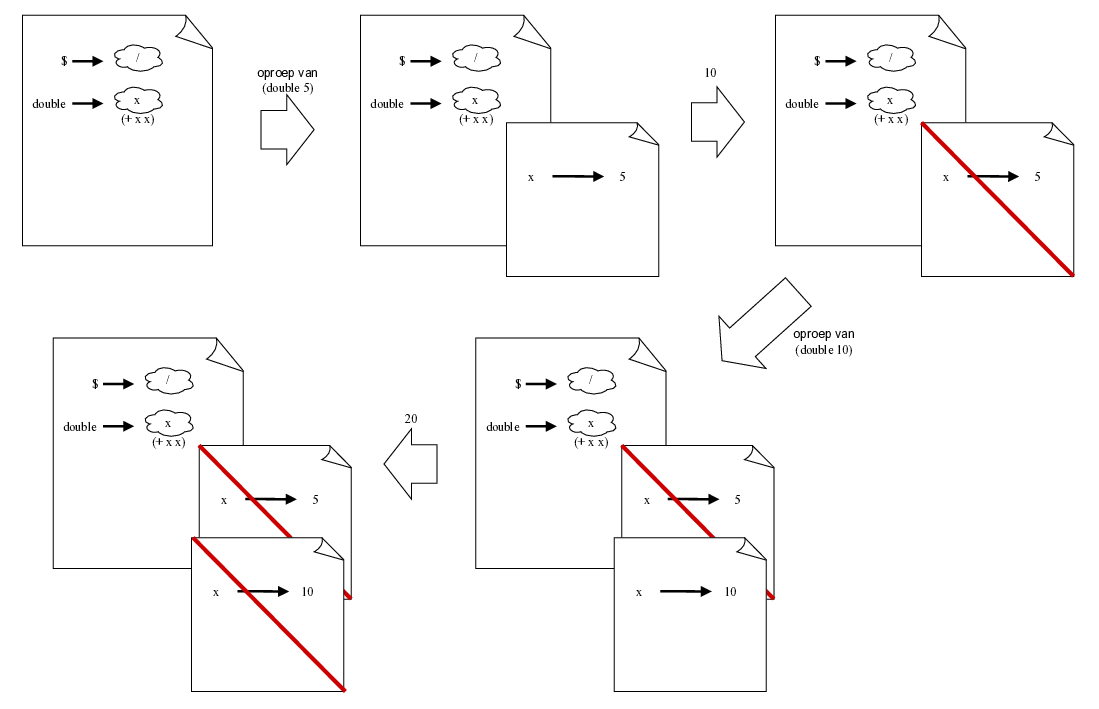
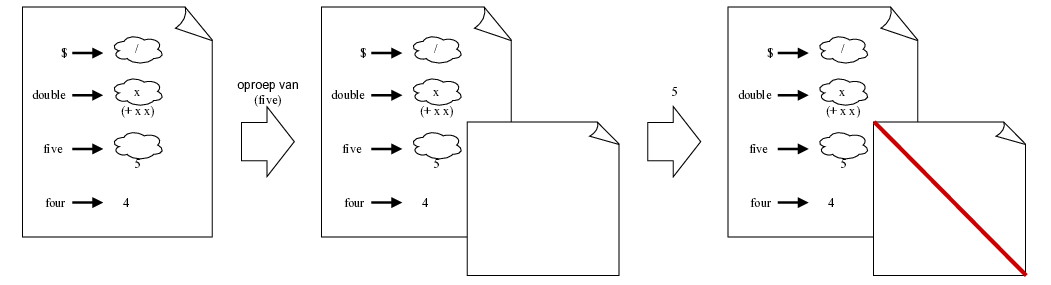
> (define (five) 5)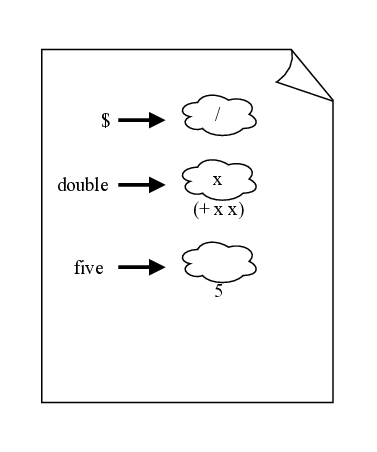
> (define four 4)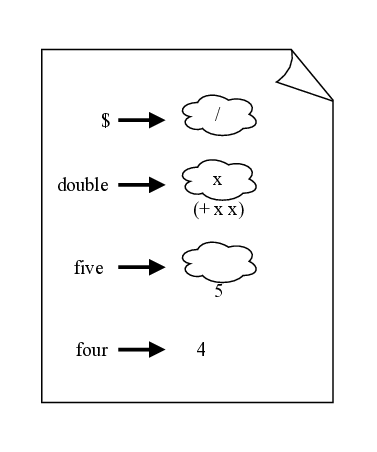
> (four)
application: not a procedure;
expected a procedure that can be applied to arguments
given: 4
arguments...: [none]
> (five)
5

2.4 fourth

Schrijf een procedure die de vierde macht van zijn argument berekent. Doe dit op twee verschillende manieren, eerst eens door gebruik te maken van de vermenigvuldiging en dan eens door square te gebruiken. Noem de versie die de vermenigvuldiging gebruikt (fourth-* x). Noem de versie die square gebruikt (fourth-square x).

(define (square x) (* x x))

(define (fourth-* x)
(* x x x x))

(define (fourth-square x)
(square (square x)))

> (fourth-* -2)
16

> (fourth-square -2)
16

2.5 sum-3-squares

Schrijf een procedure sum-3-squares die drie getallen als argumenten neemt en de som van hun kwadraten teruggeeft.

(define (sum-3-squares a b c)
(+ (square a) (square b) (square c)))

> (sum-3-squares 2 -2 3)
17

2.6 Celsius naar Fahrenheit

Schrijf een procedure convert-C-to-F die een temperatuur in graden Celsius omzet in graden Fahrenheit. Gebruik hiervoor de formule: $F = (C + 40)\times 1.8 - 40$.

(define (convert-C-to-F c)
(- (* (+ c 40) 1.8) 40))

> (convert-C-to-F 36)
96.80000000000001

2.7 Evaluatie van eenvoudige procedures

Deze oefening is gebaseerd op oefening 4.4 uit Simply Scheme

Elk van de volgende procedure-definities bevat een bepaalde fout. Geef aan wat fout is en corrigeer.

(define (sphere-volume r) (* (/ 4 3) 3.14) (* r r r))
(define (sphere-volume-correct r)
(* (* r r r)
(* (/ 4 3) 3.14)))
(define (next x) (x + 1))
(define (next-correct x)
(+ x 1))
(define (square) (* x x))
(define (square x)
(* x x))
(define (triangle-area triangle) (* 0.5 base height))
(define (triangle-area-correct base height)
(* 0.5 base height))
(define (sum-of-squares (square x) (square y)) (+ (square x) (square y)))
(define (sum-of-squares-correct x y)
(+ (square x) (square y)))

2.8 Omgevingsmodel met Atoma-schriftjes

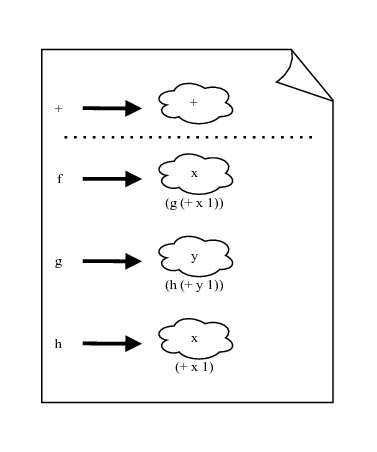
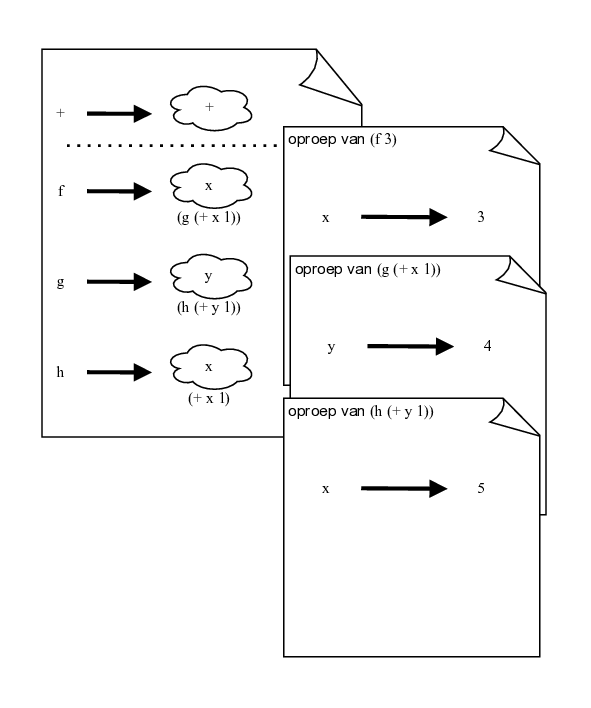
Voor deze oefening maken we gebruik van de metafoor met Atoma-shriftjes. Gegeven zijn de volgende definities:

(define (f x)
  (g (+ x 1)))

(define (g y)
  (h (+ y 1)))

(define (h x)
  (+ x 1))

Teken de status van de Atoma-schrift net nadat de definities zijn uitgevoerd.
Teken vervolgens de status van de Atoma-schrift net nadat h haar resultaat teruggeeft bij de oproep van (f 3).

2.9 Omgevingsmodel met Atoma-schriftjes: sum

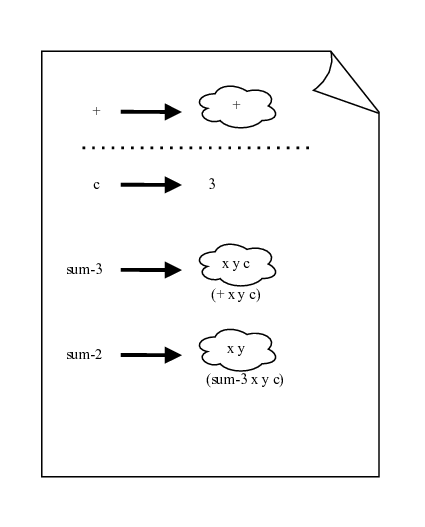
Voor deze oefening maken we gebruik van de metafoor met Atoma-shriftjes. Gegeven zijn de volgende definities:

(define c 3)

(define (sum-3 x y c)
(+ x y c))

(define (sum-2 x y)
(sum-3 x y c))

Teken de status van de Atoma-schrift net nadat de definities zijn uitgevoerd.
Teken vervolgens de status van de Atoma-schrift net nadat sum-3 haar resultaat teruggeeft bij de oproep van (sum-2 1 2).

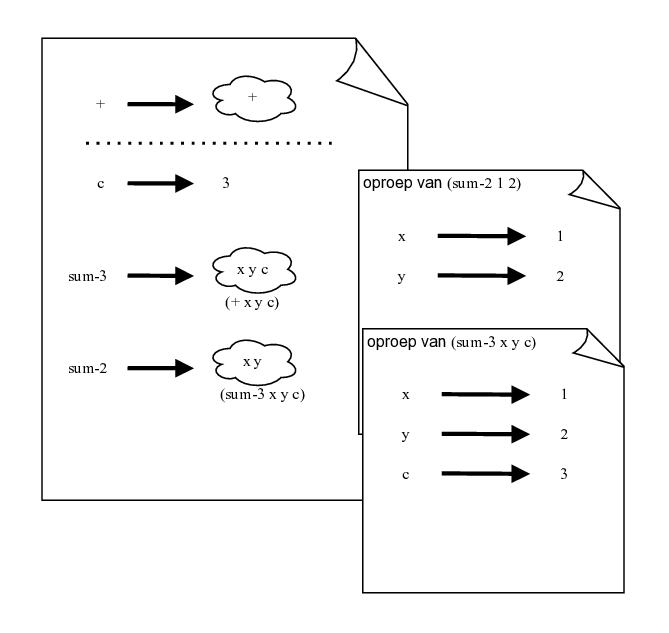
2.10 Discount

Deze oefening is gebaseerd op oefening 4.9 uit Simply Scheme

Schrijf een procedure (discount prijs korting) die twee argumenten heeft: de initiële prijs van een item en het kortingspercentage. De procedure moet de nieuwe prijs teruggeven:

(define (discount prijs korting)
(* prijs (/ (- 100 korting) 100.0)))

> (discount 10 5)
9.5
> (discount 29.9 50)
14.95

2.11 Extra Oefeningen

2.11.1 Fahrenheit naar Celsius

Schrijf een procedure convert-F-to-C die een temperatuur in graden Fahrenheit omzet in graden Celsius.

(define (convert-F-to-C f)
(- (/ (+ f 40) 1.8) 40))

> (convert-F-to-C 96.8)
36.0

2.11.2 Abstractie van procedures

2.11.2.1 Oppervlakte en Omtrek

In het hoorcollege kwamen volgende procedures aan bod om de oppervlakte en omtrek van een cirkel te berekenen:

(define pi 3.14159)

(define (opp-cirkel r)
(* r r pi))

(define (omtrek-cirkel r)
(* 2 pi r))

Schrijf zelf procedures om de oppervlakte en omtrek van een driehoek en een vierkant te berekenen. Schrijf de procedures:

(opp-driehoek b h)
(define (opp-driehoek b h)
(/ (* b h) 2))
(omtrek-driehoek z1 z2 z3)
(define (omtrek-driehoek z1 z2 z3)
(+ z1 z2 z3))
(opp-vierkant z)
(define (opp-vierkant z)
(* z z))
(omtrek-vierkant z)
(define (omtrek-vierkant z)
(* z 4))

2.11.2.2 Oppervlakte en Inhoud

In het hoorcollege werden de procedures uit de vorige oefening hergebruikt om de oppervlakte van ruimtefiguren zoals cilinders, kegels en bollen te berekenen:

(define (opp-cylinder r h)
  (+ (* h (omtrek-cirkel r))
     (* 2 (opp-cirkel r))))

(define (kwadraat x) (* x x))

(define (opp-kegel r h)
  (+ (opp-cirkel r)
     (* pi r (sqrt (+ (kwadraat r) (kwadraat h))))))

(define (opp-bol r)
  (* 4 pi (kwadraat r)))

Schrijf zelf procedures om de oppervlakte en inhoud van enkele andere ruimtefiguren te berekenen. Maak waar mogelijk gebruik van abstractie, door de procedures uit de vorige oefening te hergebruiken. Schrijf de procedures:

(opp-balk l b h)
(define (opp-balk l b h)
  (+ (* l b 2)
     (* l h 2)
     (* b h 2)))
(inhoud-balk l b h)
(define (inhoud-balk l b h)
(* l b h))
(inhoud-bol r)
(define (inhoud-bol r)
(* 4/3 pi (expt r 3)))
(inhoud-cilinder h r)
(define (inhoud-cilinder h r)
(* (opp-cirkel r) h))

2.11.3 Wetenschappelijke notatie

Deze oefening is gebaseerd op oefening 4.8 uit Simply Scheme

De wetenschappelijke notatie van een getal is een manier om zeer grote of zeer kleine getallen weer te geven als een aantal malen een gehele macht van 10. Zulk een getal wordt weergegeven in de vorm $\pm a \times 10^b$, waarbij $a$ de coëfficient wordt genoemd en $b$ de exponent.

Bijvoorbeeld, $5 \times 10^7$ representeert het getal 50000000, en $3.26 \times 10^{-9}$ drukt het getal 0.00000000326 uit in wetenschappelijke notatie.

2.11.3.1 Van wetenschappelijke notatie naar een getal

Schrijf een procedure (scientific coefficient exponent) met twee argumenten: het eerste stelt de coëfficient voor en het tweede de exponent. Bij het oproepen zal de procedure het getal voluit teruggeven.

Je kan hierbij gebruik maken van de procedure (expt n e) die $n^e$ uitrekent. Merk op dat sommige versies van Scheme breuken als a/b weergeen. Andere versies gebruiken de wetenschappelijke notatie. Dus het laatste voorbeeld kan gerepresenteerd worden als "21/5000" of "4.2E-4" in plaats van 0.00042.

(define (scientific coefficient exponent)
(exact->inexact (* coefficient (expt 10 exponent))))

> (scientific 7 3)
7000.0
> (scientific 42 -5)
0.00042

2.11.3.2 Van getal naar wetenschappelijke notatie

Schrijf nu de nodige procedures om van een volledig getal naar wetenschappelijke notatie te gaan. De eerste procedure (sci-exponent getal) berekent van het gegeven getal de exponent, de tweede procedure (sci-coefficient getal) berekent de coëfficient.

Je kan gebruik maken van de primitieve procedures log en floor.

(define (sci-exponent getal)
(floor (/ (log getal) (log 10))))

(define (sci-coefficient getal)
(/ getal (expt 10 (sci-exponent getal))))

Merk op dat (sci-exponent 1000) niet het gewenste resultaat oplevert.
> (sci-exponent 1000)
2.0
We krijgen 2 als resultaat, maar verwachten eigenlijk 3. Dit komt omdat computers kommagetallen niet exact kunnen voorstellen.
> (/ (log 1000) (log 10))
2.9999999999999996
We zien hier een eerste keer een voorbeeld van een afrondingsfout door de scheme-interpreter.

> (sci-coefficient 7000)
7.0
> (sci-exponent 7000)
3.0

2.11.4 Fooi (tip)

Deze oefening is gebaseerd op oefening 4.10 uit Simply Scheme

Schrijf een procedure (tip bedrag) om de fooi te berekenen die je in een restaurant zou geven. Deze procedure neemt als argument het totaalbedrag en geeft het fooibedrag terug. De fooi is 15% van het totale bedrag maar de procedure moet kunnen afronden zodanig dat het totale geldbedrag (dus de originele prijs plus fooi) een geheel aantal euro’s is. Gebruik de procedure ceiling om naar boven af te ronden.

(define (tip bedrag)
(- (ceiling (+ bedrag (* 0.15 bedrag))) bedrag))

> (tip 19.98)
3.0199999999999996
> (tip 29.23)
4.77
> (tip 7.54)
1.46

← prev up next →

1	Inleiding
2	Eenvoudige Procedures
3	Complexe Procedures
4	Soorten Recursie en Soorten Processen
5	Lijsten en symbolische data
6	Hogere Orde Procedures
7	Imperatief Programmeren
8	Abstracte Data Types
9	Closures en Omgevingsdiagrammen
10	Objectgebaseerd Programmeren
11	Bomen
12	Stromen

2.1	Prefixnotatie
2.2	Voorspel het resultaat van eenvoudige expressies
2.3	Voorspel het resultaat van eenvoudige expressies a.d.h.v. omgevingsmodellen
2.4	fourth
2.5	sum-3-squares
2.6	Celsius naar Fahrenheit
2.7	Evaluatie van eenvoudige procedures
2.8	Omgevingsmodel met Atoma-schriftjes
2.9	Omgevingsmodel met Atoma-schriftjes: sum
2.10	Discount
2.11	Extra Oefeningen