5 Lijsten en symbolische data
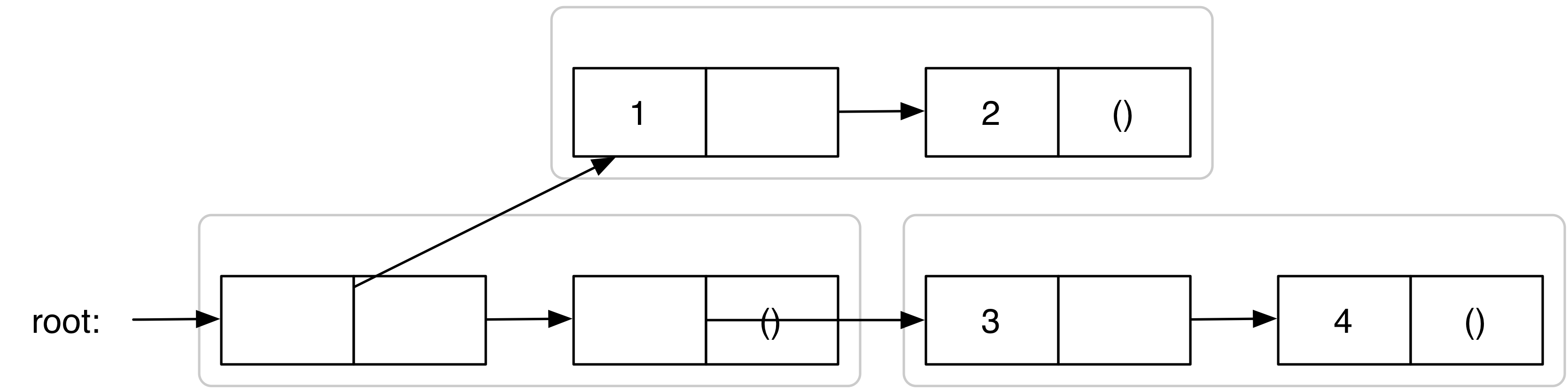
5.1 Box-and-pointer representatie
(list 1 2) (cons 1 (list 2)) (cons 1 (cons 2 '())) (list (list 1 2) (list 3 4)) (list 1 2 (cons 3 (cons 4 5)))
5.2 Voorspel
Deze oefening is gebaseerd op oefening 2.53 van Structure and Interpretation of Computer Programs
> (list 'a 'b 'c) (a b c)
> (list (list 'george)) ((george))
> (cdr '((x1 x2) (y1 y2))) ((y1 y2))
> (cadr '((x1 x2) (y1 y2))) (y1 y2)
> (atom? (car '(a short list))) #t
> (memq 'red '((red shoes) (blue socks))) #f
> (memq 'red '(red shoes blue socks)) (red shoes blue socks)
De atom? procedure is als volgt gedefinieerd:
(define (atom? x) (not (pair? x)))
5.3 Lijsten met procedures en symbolen
(define p (list cons +)) (define q '(cons +)) (define r (list 'cons '+))
> ((car p) 3 4) (3 . 4)
> ((cadr p) 3 4) 7
> ((car r) 3 4) application: not a procedure;
expected a procedure that can be applied to arguments
given: 'cons
arguments...:
3
4
> ((cadr q) 3 4) application: not a procedure;
expected a procedure that can be applied to arguments
given: '+
arguments...:
3
4
5.4 Recursie/iteratie op lijsten: modeloplossing
Het volgende stukje "code" beschrijft een standaardpatroon voor recursieve procedures op lijsten. De meeste recursieve procedures op lijsten kunnen geschreven worden volgens dit patroon, of volgens een zeer gelijkaardig patroon.
(define (list-procedure-rec lst) (if (null? lst) base-result (combine-car/res (do-something-with (car lst)) (list-procedure-rec (cdr lst))))) (define (list-procedure-it lst) (define (iter lst res) (if (null? lst) res (iter (cdr lst) (combine-car/res (do-something-with (car lst)) res)))) (iter lst base-result))
5.5 Element toevoegen achteraan een lijst: add-to-end
Defineer (zonder gebruik te maken van append) een procedure (add-to-end e l) die een nieuwe lijst teruggeeft met dezelfde elementen als de lijst l maar met het object e aan het einde toegevoegd.
(define (add-to-end e l) (if (null? l) (cons e '()) (cons (car l) (add-to-end e (cdr l)))))
> (add-to-end 999 '(1 2 3 4 5)) (1 2 3 4 5 999)
> (add-to-end 999 '()) (999)
> (add-to-end 999 '(1)) (1 999)
5.6 Lijsten aaneen plakken: my-append (iteratief)
Schrijf de procedure my-append op iteratieve wijze. Doe dit zo efficiënt mogelijk.
(define (my-append lst1 lst2) (define (loop lst res) (if (null? lst) res (loop (cdr lst) (cons (car lst) res)))) (loop (reverse lst1) lst2))
> (my-append '(1 2 3) '(4 5)) (1 2 3 4 5)
> (my-append '(1 2 3) '()) (1 2 3)
> (my-append '() '(1 2 3)) (1 2 3)
> (my-append '() '()) ()
5.7 Lijsten omdraaien: my-reverse (Recursief & Iteratief)
Deze oefening is gebaseerd op oefening 2.17 van Structure and Interpretation of Computer Programs
Schrijf de procedure (rec-reverse l) die een lijst teruggeeft met dezelfde elementen als l maar in de omgekeerde volgorde.
Maak 2 versies: één die een recursief proces en één die een iteratief proces genereert. Noem de recursieve versie (rec-reverse l) en de iteratieve versie (iter-reverse l).
(define (rec-reverse l) (if (null? l) '() (append (rec-reverse (cdr l)) (list (car l)))))
(define (iter-reverse l) (define (iter l r) (if (null? l) r (iter (cdr l) (cons (car l) r)))) (iter l '()))
> (rec-reverse '(1 2 3)) (3 2 1)
> (rec-reverse '(1)) (1)
> (rec-reverse '()) ()
> (iter-reverse '(1 2 3)) (3 2 1)
> (iter-reverse '(1)) (1)
> (iter-reverse '()) ()
5.8 Laatste element van een lijst bepalen: last
Deze oefening is gebaseerd op oefening 2.16 van Structure and Interpretation of Computer Programs
Schrijf een procedure last die het laatste element van een lijst teruggeeft.
(define (last lst) (cond ((null? lst) #f) ((null? (cdr lst)) (car lst)) (else (last (cdr lst)))))
> (last '(1 2 3)) 3
> (last '(1)) 1
> (last '()) #f
5.9 Elementen in een lijstvervangen: replace
Schrijf de functie (replace e1 e2 l) die een lijst teruggeeft, gelijk aan lijst l, maar waarin alle elementen gelijk aan e1 vervangen zijn door e2. Gebruik (eq? e1 e2) om twee elementen te vergelijken. De procedure mag een recursief proces genereren.
(define (replace e1 e2 l) (cond ((null? l) l) ((eq? (car l) e1) (cons e2 (replace e1 e2 (cdr l)))) (else (cons (car l) (replace e1 e2 (cdr l))))))
> (replace 1 999 '(1 2 1 3 1 4 1 5 1)) (999 2 999 3 999 4 999 5 999)
> (replace 1 999 '(2 3 4 5 6 7)) (2 3 4 5 6 7)
> (replace 1 999 '(1)) (999)
> (replace 1 999 '()) ()
5.10 Gelijkheid van twee lijsten bepalen: my-equal?
Deze oefening is gebaseerd op oefening 2.54 van Structure and Interpretation of Computer Programs
Schrijf de procedure (my-equal? l1 l2) die nagaat of twee lijsten van symbolen l1 en l2 gelijk zijn. Gebruik (eq? e1 e2) om twee elementen te vergelijken.
(define (my-equal? l1 l2) (cond ((and (null? l1) (null? l2)) #t) ((or (null? l1) (null? l2)) #f) ((eq? (car l1) (car l2)) (my-equal? (cdr l1) (cdr l2))) (else #f)))
> (my-equal? '(1 2 3) '(1 2 3)) #t
> (my-equal? '(1 2 3) '(4 5 6)) #f
> (my-equal? '(1 2 3) '(1 2)) #f
> (my-equal? '(1 2 3) '()) #f
> (my-equal? '() '(1 2 3)) #f
5.11 Element tussenvoegen in een lijst: intersperse
Definieer een procedure (intersperse e l) die een nieuwe lijst teruggeeft met dezelfde elementen als de lijst l, maar met het object e tussengevoegd tussen elk van de originele elementen.
(define (intersperse e l) (cond ((null? l) '()) ((null? (cdr l)) l) (else (cons (car l) (cons e (intersperse e (cdr l)))))))
> (intersperse 1 '(3 4 5)) (3 1 4 1 5)
> (intersperse 1 '(9)) (9)
> (intersperse 1 '()) ()
5.12 Sommatie van elementen in lijsten: sum-lists
De procedure (sum-lists l1 l2) heeft als argumenten 2 lijsten met getallen, en geeft een lijst terug met de sommen van de overeenkomstige elementen van de input-lijsten.
Merk op dat de twee input-lijsten niet dezelfde lengte hoeven te hebben. In dat geval worden de resterende elementen van de langste lijst gewoon overgenomen.
5.12.1 Recursieve versie
Schrijf een recursieve versie, noem het (rec-sum-lists l1 l2).
(define (rec-sum-lists l1 l2) (cond ((null? l1) l2) ((null? l2) l1) (else (cons (+ (car l1) (car l2)) (rec-sum-lists (cdr l1) (cdr l2))))))
> (rec-sum-lists '(1 2 3 4) '(5 6 7)) (6 8 10 4)
> (rec-sum-lists '(1 2 3 4) '()) (1 2 3 4)
> (rec-sum-lists '() '(1 2 3)) (1 2 3)
5.12.2 Iteratieve versie
Schrijf een iteratieve versie, noem het (iter-sum-lists l1 l2).
(define (iter-sum-lists l1 l2) (define (iter lst1 lst2 res) (cond ((and (null? lst1) (null? lst2)) (reverse res)) ((null? lst1) (iter lst1 (cdr lst2) (cons (car lst2) res))) ((null? lst2) (iter (cdr lst1) lst2 (cons (car lst1) res))) (else (iter (cdr lst1) (cdr lst2) (cons (+ (car lst1) (car lst2)) res))))) (iter l1 l2 '()))
of
(define (iter-sum-lists l1 l2) (define (iter l1 l2 res) (cond ((null? l1) (append (reverse res) l2)) ((null? l2) (append (reverse res) l1)) (else (iter (cdr l1) (cdr l2) (cons (+ (car l1) (car l2)) res))))) (iter l1 l2 '()))
> (iter-sum-lists '(1 2 3 4) '(5 6 7)) (6 8 10 4)
> (iter-sum-lists '(1 2 3 4) '()) (1 2 3 4)
> (iter-sum-lists '() '(1 2 3)) (1 2 3)
5.13 Lijsten samenvoegen
5.13.1 Samenvoegen van twee lijsten: merge-n
Schrijf een procedure die 2 lijsten samenvoegt tot 1 enkele lijst door telkens n elementen van de eerste lijst te laten volgen door n elementen van de tweede lijst, enzovoort. Indien er minder dan n elementen overblijven in een lijst, neem je alles wat er overblijft. Doe dit zowel op recursieve als iteratieve wijze. Noem de recursieve versie (rec-merge-n lst1 lst2 n). Noem de iteratieve versie (iter-merge-n lst1 lst2 n).
(define (rec-merge-n lst1 lst2 n) (define (merge l1 l2 i) (cond ((null? l1) l2) ((= i n) (merge l2 l1 0)) (else (cons (car l1) (merge (cdr l1) l2 (+ i 1)))))) (merge lst1 lst2 0))
Een oudere oplossing uit de oefeningenbundel doet het ietsje anders. Bij deze oplossing wordt er gebruik gemaakt van een hulpprocedure geef-n+rest die, gegeven een lijst en een getal, 2 resultaten geeft: de eerste n elementen van de lijst, en de rest van de lijst. De 2 resultaten worden teruggegeven door gebruik te maken van een pair.
(define (rec-merge-n lst1 lst2 n) (define (geef-n+rest lst n) (cond ((or (= 0 n) (null? lst)) (cons '() lst)) (else (let* ((res (geef-n+rest (cdr lst) (- n 1))) (first (car res)) (rest (cdr res))) (cons (cons (car lst) first) rest))))) (cond ((null? lst1) lst2) ((null? lst2) lst1) (else (let* ((n-lst1 (geef-n+rest lst1 n)) (n-lst2 (geef-n+rest lst2 n)) (n-lst1-first (car n-lst1)) (n-lst1-rest (cdr n-lst1)) (n-lst2-first (car n-lst2)) (n-lst2-rest (cdr n-lst2))) (append (append n-lst1-first n-lst2-first) (rec-merge-n n-lst1-rest n-lst2-rest n))))))
> (rec-merge-n '(1 2 3 4 5) '(6 7 8 9) 2) (1 2 6 7 3 4 8 9 5)
> (rec-merge-n '(1 2 3 4 5) '(6 7 8 9) 3) (1 2 3 6 7 8 4 5 9)
> (rec-merge-n '(1 2) '(3 4 5 6) 4) (1 2 3 4 5 6)
De nieuwe en oude oplossing genereren beiden een recursief process aangezien er gebruik gemaakt wordt van constructieve recursie. Bij de oude oplossing genereren zowel geef-n+rest als merge-n een recursief proces. Nadat de laatste recursieve oproep gedaan is moet het resultaat nog opgebouwd worden (constructieve recursie). Hieronder geven we de iteratieve versies.
(define (iter-merge-n lst1 lst2 n) (define (merge l1 l2 i res) (cond ((null? l1) (append (reverse res) l2)) ((= i n) (merge l2 l1 0 res)) (else (merge (cdr l1) l2 (+ i 1) (cons (car l1) res))))) (merge lst1 lst2 0 '()))
Oude oplossing:
(define (iter-merge-n lst1 lst2 n) (define (geef-n+rest lst n) (define (iter lst n res) (cond ((or (null? lst) (= 0 n)) (cons res lst)) (else (iter (cdr lst) (- n 1) (append res (list (car lst))))))) (iter lst n '())) (define (iter-merge lst1 lst2 res) (cond ((null? lst1) (append res lst2)) ((null? lst2) (append res lst1)) (else (let* ((n-lst1 (geef-n+rest lst1 n)) (n-lst2 (geef-n+rest lst2 n)) (n-lst1-first (car n-lst1)) (n-lst1-rest (cdr n-lst1)) (n-lst2-first (car n-lst2)) (n-lst2-rest (cdr n-lst2))) (iter-merge n-lst1-rest n-lst2-rest (append res (append n-lst1-first n-lst2-first))))))) (iter-merge lst1 lst2 '()))
> (iter-merge-n '(1 2 3 4 5) '(6 7 8 9) 2) (1 2 6 7 3 4 8 9 5)
> (iter-merge-n '(1 2 3 4 5) '(6 7 8 9) 3) (1 2 3 6 7 8 4 5 9)
> (iter-merge-n '(1 2) '(3 4 5 6) 4) (1 2 3 4 5 6)
5.13.2 Samenvoegen van een willekeurig aantal lijsten: super-merge-n
Veralgemeen de procedure uit Samenvoegen van twee lijsten: merge-n tot een procedure (super-merge-n lsts n) die een willekeurig aantal lijsten samenvoegt door achtereenvolgens n elementen van elke lijst te nemen. De lijsten zitten samen in de formele parameter lsts.
(define (super-merge-n lsts n) (define (merge current rest i) (cond ((and (null? current) (null? rest)) '()) ((null? current) (merge (car rest) (cdr rest) 0)) ((= i n) (merge (car rest) (append (cdr rest) (list current)) 0)) (else (cons (car current) (merge (cdr current) rest (+ i 1)))))) (if (null? lsts) '() (merge (car lsts) (cdr lsts) 0)))
Oude oplossing:
(define (super-merge-n lsts n) (define (geef-n+rest lst n) (cond ((or (= 0 n) (null? lst)) (cons '() lst)) (else (let* ((res (geef-n+rest (cdr lst) (- n 1))) (first (car res)) (rest (cdr res))) (cons (cons (car lst) first) rest))))) (if (null? lsts) '() (let* ((g-n+rest (geef-n+rest (car lsts) n)) (first (car g-n+rest)) (rest (cdr g-n+rest))) (append first (super-merge-n (append (cdr lsts) (if (null? rest) rest (list rest))) n)))))
> (super-merge-n '((a b c d e f) (g h i j k) (l m n o p q) (r s t u v w)) 3) (a b c g h i l m n r s t d e f j k o p q u v w)
5.14 Extra Oefeningen
5.14.1 Pairs als procedures
Deze oefening is gebaseerd op oefening 2.4 van Structure and Interpretation of Computer Programs
Het is mogelijk om pairs, net zoals getallen en andere vormen van data, voor te stellen als procedures:
(define (my-cons x y) (lambda (m) (m x y))) (define (my-car z) (z (lambda (p q) p)))
> (my-car (my-cons 1 2)) 1
5.14.1.1 Definitie van my-cdr
Vervolledig de definities van hierboven door my-cdr te implementeren.
(define (my-cdr z) (z (lambda (p q) q)))
5.14.2 replace d.m.v. map
Implementeer de procedure replace-dmv-map, door middel van de ingebouwde procedure map.
(define (replace-dmv-map e1 e2 l) (map (lambda (x) (if (eq? x e1) e2 x)) l))
> (replace-dmv-map 1 999 '(1 2 1 3 1 4 1 5 1)) (999 2 999 3 999 4 999 5 999)
> (replace-dmv-map 1 999 '(2 3 4 5 6 7)) (2 3 4 5 6 7)
> (replace-dmv-map 1 999 '(1)) (999)
> (replace-dmv-map 1 999 '()) ()
5.14.3 Combine over list
(define (map a-function a-list) (if (null? a-list) '() (cons (a-function (car a-list)) (map a-function (cdr a-list)))))
(define (combine-over-list op unity a-list) (if (null? a-list) unity (op (car a-list) (combine-over-list op unity (cdr a-list)))))
- van een lijst van getallen de som van de kwadraten te berekenen. Definieer hiervoor een procedure (som-van-de-kwadraten list).
(define (square x) (* x x)) (define (som-van-de-kwadraten list) (combine-over-list + 0 (map square list))) - te testen of een lijst uitsluitend oneven getallen omvat. Definieer hiervoor een procedure (uitsluitend-oneven? list).
(define (my-and a b) (and a b)) (define (uitsluitend-oneven? list) (combine-over-list my-and #true (map odd? list)))
> (som-van-de-kwadraten '(1 2 3)) 14
> (uitsluitend-oneven? '(2 3)) #f
> (uitsluitend-oneven? '(1 3)) #t
5.14.4 Examen Informatica eerste zit 1999
5.14.4.1 Dissectie van een lijst
Schrijf een procedure die een lijst dissecteert in een nieuwe lijst door afwisselend n elementen dan weer wel en dan weer niet te behouden. Indien er minder dan n elementen overblijven in de lijst, neem je alles wat er overblijft. Doe dit zowel op recursieve als iteratieve wijze. Noem de recursieve versie (rec-dissect-n lst n). Noem de iteratieve versie (iter-dissect-n lst n).
(define (rec-dissect-n lst n) (define (dissecter lst i remove?) (cond ((null? lst) '()) ((= i n) (dissecter lst 0 (not remove?))) (remove? (dissecter (cdr lst) (+ i 1) remove?)) (else (cons (car lst) (dissecter (cdr lst) (+ i 1) remove?))))) (dissecter lst 0 #f))
> (rec-dissect-n '(1 2 3 4 5) 2) (1 2 5)
> (rec-dissect-n '(1 2 3 4 5 6 7 8) 3) (1 2 3 7 8)
> (rec-dissect-n '(1 2) 4) (1 2)
(define (iter-dissect-n lst n) (define (iter lst i remove? result) (cond ((null? lst) (reverse result)) ((= i n) (iter lst 0 (not remove?) result)) (remove? (iter (cdr lst) (+ i 1) remove? result)) (else (iter (cdr lst) (+ i 1) remove? (cons (car lst) result))))) (iter lst 0 #f '()))
> (iter-dissect-n '(1 2 3 4 5) 2) (1 2 5)
5.14.4.2 Splitsen van een lijst
Schrijf een procedure (split lst n) die niet alleen de gedissecteerde lijst uit Dissectie van een lijst teruggeeft, maar ook een lijst die opgebouwd is uit de resten van de oorspronkelijke lijst.
(define (split lst n) (define (splitter l i drop? resA resB) (cond ((null? l) (list (reverse resA) (reverse resB))) ((= i n) (splitter l 0 (not drop?) resA resB)) (drop? (splitter (cdr l) (+ i 1) drop? resA (cons (car l) resB))) (else (splitter (cdr l) (+ i 1) drop? (cons (car l) resA) resB)))) (splitter lst 0 #f '() '()))
> (split '(1 2 3 4 5 6 7 8 9 10) 2) ((1 2 5 6 9 10) (3 4 7 8))
5.14.4.3 Splitsen van meerdere lijsten
Veralgemeen de procedure uit Splitsen van een lijst tot een procedure (super-split lsts n) die een willekeurig aantal lijsten split. De lijsten zitten samen in de formele paramater lsts. Als resultaat worden twee lijsten van lijsten teruggegeven. De eerste lijst bestaat uit alle gedissecteerde lijsten uit Dissectie van een lijst, de tweede lijst bevat de restjes.
(define (super-split lsts n) (let ((first (map (lambda (l) (car (split l n))) lsts)) (rest (map (lambda (l) (cadr (split l n))) lsts))) (list first rest)))
> (super-split '((a b c d e f) (g h i j k) (l m n o p q) (r s t u v w)) 3) (((a b c) (g h i) (l m n) (r s t)) ((d e f) (j k) (o p q) (u v w)))
5.14.5 Examen Informatica Partieel januari 1994
5.14.5.1 Kopie van een lijst, zonder elementen in een interval
Schrijf een lineair recursieve procedure all-but-interval die een kopie neemt van een geordende lijst getallen, uitgezonderd die getallen binnen een bepaald interval. Je mag ervan uitgaan dat elk getal in de lijst strikt groter is dan zijn voorganger (er komen geen dubbels voor in de lijst). Er worden twee parameters doorgegeven om het interval aan te duiden, en de eerste is kleiner of gelijk aan de tweede.
(define (all-but-interval l start stop) (cond ((null? l) l) ((> (car l) stop) l) ((< (car l) start) (cons (car l) (all-but-interval (cdr l) start stop))) (else (all-but-interval (cdr l) start stop))))
> (all-but-interval '(1 2 3 4 5) 2 4) (1 5)
> (all-but-interval '(1 2 3 4 5) 0 7) ()
> (all-but-interval '(1 2 3 4 5) 1 1) (2 3 4 5)
5.14.5.2 Iteratieve versie
Schrijf een iteratieve versie van dezelfde procedure. Noem het (iter-all-but-interval l start stop).
(define (iter-all-but-interval l start stop) (define (iter l acc) (cond ((null? l) (reverse acc)) ((> (car l) stop) (append (reverse acc) l)) ((< (car l) start) (iter (cdr l) (cons (car l) acc))) (else (iter (cdr l) acc)))) (iter l '()))
> (iter-all-but-interval '(1 2 3 4 5) 2 4) (1 5)
> (iter-all-but-interval '(1 2 3 4 5) 0 7) ()
> (iter-all-but-interval '(1 2 3 4 5) 1 1) (2 3 4 5)
5.14.5.3 Zelfde oefening voor een lijst waar dubbels in voorkomen.
Moet je de procedure veranderen als er wel dubbels in de lijst mogen voorkomen? Zo ja, herschrijf de eerste versie. Zo nee, waarom niet?
Neen, alles blijft hetzelfde.
> (all-but-interval '(1 2 2 2 3 4 4 5 5) 2 4) (1 5 5)
5.14.6 Examen Informatica Partieel januari 1996
Veronderstel dat we woorden voorstellen als lijsten van symbolen. Bijvoorbeeld het woordje "computer" wordt voorgesteld door de lijst (c o m p u t e r). Veronderstel bovendien dat je beschikt over een predicaat klinker? dat #t geeft indien een symbool een klinker voorstelt, en #f in alle andere gevallen.
(define (klinker? x) (or (eq? x 'a) (eq? x 'e) (eq? x 'i) (eq? x 'o) (eq? x 'u)))
5.14.6.1 Procedure p-taal
Schrijf een procedure die als invoer zo’n woord neemt, en dit "vertaalt" in de "p-taal" door elke klinker te vervangen door diezelfde klinker, gevolgd door een 'p, en dan nog eens die klinker. Doe dit zowel op recursieve als iteratieve wijze. Noem de recursieve versie (rec-p-taal woord). Noem de iteratieve versie (iter-p-taal woord). Welke van de twee versies is het snelst?
(define (rec-p-taal woord) (if (null? woord) '() (append (let ((letter (car woord))) (if (klinker? letter) (list letter 'p letter) (list letter))) (rec-p-taal (cdr woord)))))
> (rec-p-taal '(c o m p u t e r)) (c o p o m p u p u t e p e r)
> (rec-p-taal '(w e t e n s c h a p p e n)) (w e p e t e p e n s c h a p a p p e p e n)
De vorige was recursief. Performantie: O(n) want de lijst 1 keer element per element doorlopen, en telkens een lijstje van lengte 1 of 3 eraan appenden.
(define (iter-p-taal woord) (define (iter rest result) (if (null? rest) (reverse result) (iter (cdr rest) (append (let ((letter (car rest))) (if (klinker? letter) (list letter 'p letter) (list letter))) result)))) (iter woord '()))
Bovenstaande iteratieve versie is iets minder performant, maar is ook O(n). Het enige verschil met de recursieve is dat hier op het einde nog moet gereversed worden en bij de recursieve niet. Dus iets trager maar zelfde orde. Opmerking: de iteratieve is natuurlijk wel beter wat betreft geheugengebruik.
Ziehier een "slechte" iteratieve versie die O(n*n) performantie heeft:
(define (p-taal woord) (define (iter rest result) (if (null? rest) result (iter (cdr rest) (append result (let ((letter (car rest))) (if (klinker? letter) (list letter 'p letter) (list letter))))))) (iter woord '()))
De reden dat deze iteratieve versie veel slechter is dan de vorige iteratieve versie is omdat hier telkens de append gebeurt van een steeds langer wordende lijst aan een lijstje van maximaal lengte 3. De performantie van de append is echter rechtevenredig met de lengte van de eerste lijst. Dus de globale snelheidsperformantie is O(n*n) door een toepassing van een formule a la 1+2+3+4+...+n = n(n-1)/2
> (iter-p-taal '(c o m p u t e r)) (c o p o m p u p u t e p e r)
5.14.7 Examen Informatica Partieel januari 1997
Veronderstel dat we een woord voorstellen als een opeenvolging van symbolen in een lijst. Bijvoorbeeld "hottentottententen" wordt voorgesteld als '(h o t t e n t o t t e n t e n t e n).
5.14.7.1 Tel opeenvolging van letters
Schrijf een procedure die telt hoeveel keer 2 gegeven letters onmiddellijk na elkaar in een gegeven woord voorkomen. Doe dit zowel op recursieve als iteratieve wijze. Noem de recursieve versie (rec-count-2-consecutive woord). Noem de iteratieve versie (iter-count-2-consecutive woord).
(define (rec-count-2-consecutive first second lst) (define (count previous lst) (if (null? lst) 0 (let ((current (car lst))) (+ (if (and (equal? previous first) (equal? current second)) 1 0) (count current (cdr lst)))))) (if (null? lst) 0 (count (car lst) (cdr lst))))
> (rec-count-2-consecutive 'n 't '(h o t t e n t o t t e n t e n t e n)) 3
> (rec-count-2-consecutive 'e 'n '(h o t t e n t o t t e n t e n t e n)) 4
(define (iter-count-2-consecutive first second lst) (define (count previous lst ctr) (if (null? lst) ctr (let ((current (car lst)) (rest (cdr lst))) (if (and (equal? previous first) (equal? current second)) (count current rest (+ ctr 1)) (count current rest ctr))))) (if (null? lst) 0 (count (car lst) (cdr lst) 0)))
> (iter-count-2-consecutive 'n 't '(h o t t e n t o t t e n t e n t e n)) 3
> (iter-count-2-consecutive 'e 'n '(h o t t e n t o t t e n t e n t e n)) 4
5.14.7.2 Veralgemening
Veralgemeen naar keuze één van je procedures uit Tel opeenvolging van letters tot een procedure count-n-consecutive die als invoer een lijst van letters en een woord krijgt, en telt hoeveel keer de gegeven sequentie van letters in het woord voorkomt.
Let op! Hou rekening met het feit dat in een woord zoals "barbapapa" de combinatie van letters "apa" twee keer voorkomt, maar dat de combinaties elkaar overlappen. De letter "a" die in de ene combinatie (barbapapa) als laatste letter wordt gebruikt, wordt in de tweede combinatie (barbapapa) als eerste letter gebruikt.
(define (count-n-consecutive letter-list lst) (define (count lst ctr) (if (< (length lst) (length letter-list)) ctr (if (compare? letter-list lst) (count (cdr lst) (+ ctr 1)) (count (cdr lst) ctr)))) (count lst 0))
> (define (compare? letters lst) (if (null? letters) #t (and (equal? (car letters) (car lst)) (compare? (cdr letters) (cdr lst)))))
> (count-n-consecutive '(t e n) '(h o t t e n t o t t e n t e n t e n)) 4
> (count-n-consecutive '(o t t e n) '(h o t t e n t o t t e n t e n t e n)) 2
5.14.8 Examen Informatica januari 1999
5.14.8.1 Splits resultaten van een examen
Op het secretariaat van de vakgroep computerwetenschappen wil men op het einde van de examenperiode op een eenvoudige wijze een overzicht bekomen van de behaalde resultaten. De professoren dienen resultaten in door ze voor te stellen als een lijst: '("algoritmen en datastructuren" 12 8 17 15 6 15).
Het overzicht dat gevraagd wordt, splitst de puntenlijst ten opzichte van het gemiddelde. Er worden dus twee sublijsten gevormd met in de ene lijst de cijfers onder het gemiddelde en in de andere lijst de cijfers boven het gemiddelde.
Schrijf Hiervoor een procedure. Voor het vak algoritmen en datastructuren zal het overzicht er als volgt uitzien: '("algoritmen en datastructuren" (12 8 6) (17 15 15)). Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (rec-splits resultaten). Noem de iteratieve versie (iter-splits resultaten).
(define (rec-splits resultaten) (define (divide lst gem) (if (null? lst) (list '() '()) (let* ((res (divide (cdr lst) gem)) (smaller (car res)) (higher (cadr res))) (if (> (car lst) gem) (list smaller (cons (car lst) higher)) (list (cons (car lst) smaller) higher))))) (define (calc-average lst) (/ (apply + lst) (length lst))) (cons (car resultaten) (divide (cdr resultaten) (calc-average (cdr resultaten)))))
> (rec-splits '("algoritmen en datastructuren" 12 8 17 15 6 15)) ("algoritmen en datastructuren" (12 8 6) (17 15 15))
(define (iter-splits resultaten) (define (divide lst gem res) (cond ((null? lst) res) ((> (car lst) gem) (divide (cdr lst) gem (list (car res) (append (cadr res) (list (car lst)))))) (else (divide (cdr lst) gem (list (append (car res) (list (car lst))) (cadr res)))))) (define (calc-average lst) (/ (apply + lst) (length lst))) (cons (car resultaten) (divide (cdr resultaten) (calc-average (cdr resultaten)) (list '() '()))))
> (iter-splits '("algoritmen en datastructuren" 12 8 17 15 6 15)) ("algoritmen en datastructuren" (12 8 6) (17 15 15))
5.14.8.2 Overzicht voor meerdere vakken
'("1ste BA CW" ("algoritmen en datastructuren" 12 8 17 15 6 15) ("structuur van computerprogramma's" 15 18 6 12 11))
Schrijf een procedure (splits-alle lijst-resultaten) die een overzicht berekent voor alle vakken. Merk op dat er voor de verschillende vakken niet noodzakelijk evenveel cijfers zijn.
(define (splits-alle lijst-resultaten) (cons (car lijst-resultaten) (map rec-splits (cdr lijst-resultaten))))
> (splits-alle '("1ste BA CW" ("algoritmen en datastructuren" 12 8 17 15 6 15) ("structuur van computerprogramma's" 15 18 6 12 11)))
("1ste BA CW"
("algoritmen en datastructuren" (12 8 6) (17 15 15))
("structuur van computerprogramma's" (6 12 11) (15 18)))
5.14.9 Examen Informatica augustus 2009
5.14.9.1 Vergelijken van twee lijsten
Schrijf een functie die twee niet-geneste lijsten lijst1 en lijst2 als invoer neemt, en als resultaat een getal (eventueel 0) teruggeeft dat uitdrukt tot waar beide lijsten dezelfde elementen bevatten (te beginnen vanaf het eerste element). Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (rec-compare lijst1 lijst2). Noem de iteratieve versie (iter-compare lijst1 lijst2).
(define (rec-compare lijst1 lijst2) (cond ((or (null? lijst1) (null? lijst2)) 0) ((eq? (car lijst1) (car lijst2)) (+ 1 (rec-compare (cdr lijst1) (cdr lijst2)))) (else 0)))
> (rec-compare '(a b c d e f g) '(a b c x y)) 3
> (rec-compare '(x a b) '(a b c d e f g)) 0
> (rec-compare '(a b c e f g) '(a b)) 2
(define (iter-compare lijst1 lijst2) (define (loop l1 l2 res) (cond ((or (null? l1) (null? l2)) res) ((eq? (car l1) (car l2)) (loop (cdr l1) (cdr l2) (+ res 1))) (else res))) (loop lijst1 lijst2 0))
> (iter-compare '(a b c d e f g) '(a b c x y)) 3
> (iter-compare '(x a b) '(a b c d e f g)) 0
> (iter-compare '(a b c e f g) '(a b)) 2
5.14.9.2 Vergelijk twee lijsten met een bepaalde test
Schrijf een variant van de functie compare die drie argumenten als invoer neemt, namelijk lijst1, lijst2 en een willekeurige vergelijkingstest. Deze test wordt gebruikt om de elementen van de twee lijsten te vergelijken. Het resultaat van deze variant is net zoals bij de functie uit Vergelijken van twee lijsten een getal dat uitdrukt tot waar beide lijsten voldoen aan de vergelijkingstest. Noem deze versie (algemene-compare lijst1 lijst2 test).
(define (algemene-compare lijst1 lijst2 test) (cond ((or (null? lijst1) (null? lijst2)) 0) ((test (car lijst1) (car lijst2)) (+ 1 (algemene-compare (cdr lijst1) (cdr lijst2) test))) (else 0)))
5.14.9.3 Elementen groter?
Maak gebruik van de functie die je in Vergelijk twee lijsten met een bepaalde test geschreven hebt om na te gaan tot welke positie lijst1 groter is dan lijst2. Noem de procedure (compare-greater lijst1 lijst2).
(define (compare-greater lijst1 lijst2) (algemene-compare lijst1 lijst2 >))
> (compare-greater '(3 5 6 1 2 5) '(2 1 0 8 5 5)) 3
5.14.10 Examen Informatica januari 2005
Gegeven zijn 2 vlakke lijsten van dezelfde lengte. De eerste lijst is een alfabetische namenlijst, die alle namen bevat van de studenten die het vak Structuur I volgen. De tweede lijst is een puntenlijst, die uitsluitend uit getallen bestaat. Een getal op een bepaalde positie uit deze lijst is het cijfer behaald voor Structuur I door de student die op dezelfde positie in de namenlijst staat.
5.14.10.1 Geslaagd
Schrijf een functie in Scheme die met behulp van deze twee lijsten, een lijst construeert met alle namen van die studenten die 10 of meer behaalden op het vak Structuur I. Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (rec-geslaagd namen punten). Noem de iteratieve versie (iter-geslaagd namen punten).
(define (rec-geslaagd namen punten) (if (null? namen) '() (let ((res (rec-geslaagd (cdr namen) (cdr punten)))) (if (>= (car punten) 10) (cons (car namen) res) res))))
> (rec-geslaagd '(wendy dirk kris jan eef) '(12 7 10 9 18)) (wendy kris eef)
(define (iter-geslaagd namen punten) (define (geslaagd namen punten res) (cond ((null? namen) (reverse res)) ((>= (car punten) 10) (geslaagd (cdr namen) (cdr punten) (cons (car namen) res))) (else (geslaagd (cdr namen) (cdr punten) res)))) (geslaagd namen punten '()))
> (iter-geslaagd '(wendy dirk kris jan eef) '(12 7 10 9 18)) (wendy kris eef)
5.14.10.2 Algemener
Veronderstel dat de puntenlijst uitgebreid wordt naar een lijst van lijstjes. Elk deellijstje op een bepaalde positie bevat nu de cijfers voor respectievelijk de vakken Structuur I, AlgoData I, Grondslagen I en Discrete I. Deze cijfers behoren tot de student die je in de namenlijst vindt op dezelfde positie.
Schrijf een algemene functie show die gegeven de namenlijst, de uitgebreide puntenlijst en een test, een lijst construeert van alle studenten die aan deze test voldoen.
(define (show namen punten test?) (cond ((null? namen) '()) ((test? (car punten)) (cons (car namen) (show (cdr namen) (cdr punten) test?))) (else (show (cdr namen) (cdr punten) test?))))
> (show '(wendy dirk kris jan eef) '((12 13 15 18) (7 10 14 17) (10 8 7 11) (9 12 11 10) (18 14 17 19)) (lambda (punten) (and (>= (car punten) 10) (>= (cadr punten) 10) (>= (caddr punten) 10) (>= (cadddr punten) 10)))) (wendy eef)
5.14.10.3 Hergebruik
Gebruik je oplossing voor show om een functie one te schrijven die alle namen teruggeeft van die studenten die slechts 1 buiscijfer (< 10) behaalden. Bijvoorbeeld:
(define (one namen punten) (define (één-buis? punten) (if (null? punten) #f (let ((punt (car punten)) (rest (cdr punten))) (if (< punt 10) (geen-buis? rest) (één-buis? rest))))) (define (geen-buis? punten) (if (null? punten) #t (let ((punt (car punten)) (rest (cdr punten))) (if (< punt 10) #f (geen-buis? rest))))) (show namen punten één-buis?))
> (one '(wendy dirk kris jan eef) '((12 13 15 18) (7 10 14 17) (10 8 7 11) (9 12 11 10) (18 14 17 19))) (dirk jan)
5.14.11 Examen Informatica januari 2006
5.14.11.1 Comprimeer
Schrijf een procedure die een lijst temperatuursmetingen als parameter neemt en een nieuwe lijst teruggeeft waarin opeenvolgende gelijke metingen verkort worden voorgesteld. Dit gebeurt door een lijstje van 2 getallen. Het eerste getal is de eigenlijke temperatuursmeting, het tweede getal is het aantal maal dat deze meting achtereenvolgens werd waargenomen. Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (rec-comprimeer metingen). Noem de iteratieve versie (iter-comprimeer metingen).
(define (rec-comprimeer metingen) (define (hulp lst prev count) (cond ((null? lst) (list (list prev count))) ((= (car lst) prev) (hulp (cdr lst) prev (+ count 1))) (else (cons (list prev count) (hulp (cdr lst) (car lst) 1))))) (if (null? metingen) '() (hulp (cdr metingen) (car metingen) 1)))
> (rec-comprimeer '(37.5 37.5 37.2 38.0 38.0 38.0 38.3)) ((37.5 2) (37.2 1) (38.0 3) (38.3 1))
(define (iter-comprimeer metingen) (define (hulp lst prev count res) (cond ((null? lst) (reverse (cons (list prev count) res))) ((= (car lst) prev) (hulp (cdr lst) prev (+ count 1) res)) (else (hulp (cdr lst) (car lst) 1 (cons (list prev count) res))))) (if (null? metingen) '() (hulp (cdr metingen) (car metingen) 1 '())))
> (iter-comprimeer '(37.5 37.5 37.2 38.0 38.0 38.0 38.3)) ((37.5 2) (37.2 1) (38.0 3) (38.3 1))
5.14.11.2 Algemene versie voor comprimeren
Veralgemeen één van de procedures uit Comprimeer tot een procedure (comprimeer-algemeen lst op) die dezelfde compressie-operatie doet, maar nu een extra parameter op neemt, d.i. de operator waarmee de elementen op gelijkheid getest moeten worden.
(define (comprimeer-algemeen metingen test) (define (hulp lst prev count res) (cond ((null? lst) (reverse (cons (list prev count) res))) ((test (car lst) prev) (hulp (cdr lst) prev (+ count 1) res)) (else (hulp (cdr lst) (car lst) 1 (cons (list prev count) res))))) (if (null? metingen) '() (hulp (cdr metingen) (car metingen) 1 '())))
5.14.11.3 Herschrijf
Herschrijf m.b.b. de procedure comprimeer-algemeen de procedure comprimeer uit Comprimeer. Schrijf eveneens d.m.v. comprimeer-algemeen een procedure (comprimeer-zonder-decimalen metingen) die dezelfde compressie-operatie uit Comprimeer uitvoert, maar nu 2 temperatuursmetingen als gelijk beschouwt als het gehele deel voor de komma gelijk is.
(define (comprimeer metingen) (comprimeer-algemeen metingen (lambda (x y) (= x y)))) (define (comprimeer-zonder-decimalen metingen) (let ((getallen (map floor metingen))) (comprimeer-algemeen getallen (lambda (x y) (= x y)))))
> (comprimeer '(37.5 37.5 37.2 38.0 38.0 38.0 38.3)) ((37.5 2) (37.2 1) (38.0 3) (38.3 1))
> (comprimeer-zonder-decimalen '(37.5 37.5 37.2 38.0 38.0 38.0 38.3)) ((37.0 3) (38.0 4))
5.14.12 Examen Informatica januari 2008
Het is solden in de winkelketen Z&M. Bij aankoop van een jas krijg je 50% korting, bij aankoop van een kleedje 50%, bij aankoop van een rok 30% en bij aankoop van een trui 20% en voor al de rest 25%. De ontwikkelaar die de nodige software voor het kassasysteem van de winkelketen moet schrijven, stelt deze kortingen als volgt voor '((jas 50) (kleed 50) (rok 30) (trui 20)).
De aankoop van een bepaalde klant wordt eveneens in een geneste lijststructuur voorgesteld. Bvb. Jan koopt een jas van 100 euro, een trui van 25 euro, een rok van 70 euro en een T-shirt van 20 euro: '((jas 100) (trui 25) (rok 70) (t-shirt 20)).
5.14.12.1 Bereken totaal
Schrijf nu een procedure die voor de aankoop van een klant het totale bedrag berekent. Doe dit zowel op recursieve als op iteratieve wijze. Noem de recursieve versie (rec-totaal aankopen kortingen). Noem de iteratieve versie (iter-totaal aankopen kortingen).
(define (rec-totaal aankopen kortingen) (define (zoek-korting kortingen artikel) (cond ((null? kortingen) 25) ((eq? (caar kortingen) artikel) (cadar kortingen)) (else (zoek-korting (cdr kortingen) artikel)))) (if (null? aankopen) 0 (let* ((aankoop (car aankopen)) (korting (zoek-korting kortingen (car aankoop))) (prijs (cadr aankoop))) (+ (- prijs (/ (* prijs korting) 100)) (rec-totaal (cdr aankopen) kortingen)))))
> (rec-totaal '((jas 100) (trui 25) (rok 70) (t-shirt 20)) '((jas 50) (kleed 50) (rok 30) (trui 20))) 134
(define (iter-totaal aankopen kortingen) (define (zoek-korting kortingen artikel) (let ((korting (assoc artikel kortingen))) (if korting (cadr korting) 25))) (define (loop lst res) (if (null? lst) res (let* ((aankoop (car lst)) (korting (zoek-korting kortingen (car aankoop))) (prijs (cadr aankoop))) (loop (cdr lst) (+ res (- prijs (/ (* prijs korting) 100))))))) (loop aankopen 0))
> (iter-totaal '((jas 100) (trui 25) (rok 70) (t-shirt 20)) '((jas 50) (kleed 50) (rok 30) (trui 20))) 134
5.14.12.2 Herschrijf procedure totaal
Veronderstel dat er reeds een procedure korting bestaat die gegeven een artikel, de korting voor dit artikel teruggeeft. Schrijf de procedure totaal uit Bereken totaal zodanig dat de parameter korting in (totaal aankoop korting) die procedure bevat.
(define (totaal aankopen korting) (if (null? aankopen) 0 (let* ((aankoop (car aankopen)) (k (korting (car aankoop))) (prijs (cadr aankoop))) (+ (- prijs (/ (* prijs k) 100)) (totaal (cdr aankopen) korting)))))
5.14.12.3 Korting
Implementeer ook de procedure korting voor de winkelketen Z&M (m.a.w. bij aankoop van een jas rijg je 50% korting, bij aankoop van een kleedje 50%, bij aankoop van een rok 30%, bij aankoop van een trui 20% en voor al de rest 25%).
(define Z&Mkortingen '((jas 50) (kleed 50) (rok 30) (trui 20))) (define (zoek-korting kortingen artikel) (cond ((null? kortingen) 25) ((eq? (caar kortingen) artikel) (cadar kortingen)) (else (zoek-korting (cdr kortingen) artikel)))) (define (korting artikel) (zoek-korting Z&Mkortingen artikel))
> (totaal '((jas 100) (trui 25) (rok 70) (t-shirt 20)) korting) 134
5.14.13 Examen Informatica Partieel januari 1994
5.14.13.1 Filteren van elementen in een lijst
Schrijf een hogere-orde procedure filter die een gegeven predicaat loslaat op alle elementen van een lijst. Ze geeft een nieuwe lijst terug met alle elementen waarvoor het predicaat waar is.
(define (filter pred lst) (apply append (map (lambda (x) (if (pred x) (list x) '())) lst))) (define (filter pred lst) (cond ((null? lst) '()) ((pred (car lst)) (cons (car lst) (filter pred (cdr lst)))) (else (filter pred (cdr lst)))))
> (filter (lambda (x) (= (modulo x 2) 1)) '(1 2 3 4 5 6 7 8)) (1 3 5 7)
5.14.13.2 Lijst van alle niet-getallen
Gebruik de bovenstaande filter en het standaard-predicaat number? (#t als de parameter een getal is, #f in alle andere gevallen) om een procedure (filter-not-nbrs lst) te schrijven die alle NIET-getalen van een lijst teruggeeft.
(define (filter-not-nbrs lst) (filter (lambda (x) (not (number? x))) lst))
> (filter-not-nbrs '(1 a b 33 7 c)) (a b c)
5.14.13.3 Deep-filter
Herwerk filter tot een nieuwe hogere-orde procedure deep-filter die werkt op een geneste lijst. Ze maakt een nieuwe lijst met dezelfde structuur als de gegeven lijst, maar de elementen waarvoor het predicaat vals is worden vervangen door een lege lijst, de elementen waarvoor het predicaat waar is blijven staan.
(define (deep-filter pred lst) (cond ((null? lst) '()) ((pair? (car lst)) (cons (deep-filter pred (car lst)) (deep-filter pred (cdr lst)))) ((pred (car lst)) (cons (car lst) (deep-filter pred (cdr lst)))) (else (cons '() (deep-filter pred (cdr lst))))))
> (deep-filter (lambda (x) (odd? x)) '(1 2 3 (4) (5 (6 7) 8) (9) (10 (11) 12) 13 14)) (1 () 3 (()) (5 (() 7) ()) (9) (() (11) ()) 13 ())
> (deep-filter number? '(1 (a b (1)) 5)) (1 (() () (1)) 5)
5.14.13.4 Deep-filter zonder lege lijsten
Tijdens het uittesten merken we op dat bovenstaande deep-filter teveel lege lijsten produceert. Als we bijvoorbeeld deep-filter oproepen met parameters number? en '(1 (a b (1)) 5) bekomen we (1 (() () (1)) 5). Herwerk daarom deep-filter tot een deep-filter2 zodat lege lijsten waar mogelijk verwijderd worden. Als we deep-filter2 oproepen met bovenstaande parameters moeten we (1 ((1)) 5) bekomen.
(define (deep-filter2 pred lst) (cond ((null? lst) '()) ((pair? (car lst)) (cons (deep-filter2 pred (car lst)) (deep-filter2 pred (cdr lst)))) ((pred (car lst)) (cons (car lst) (deep-filter2 pred (cdr lst)))) (else (deep-filter2 pred (cdr lst)))))
> (deep-filter2 number? '(1 (a b (1)) 5)) (1 ((1)) 5)