7.8
7 Imperatief Programmeren
7.1 Vectoren transformeren: vector-map!
Schrijf een procedure (vector-map! f vec), die een bestaande
vector vec aanpast. De nieuwe elementen van deze vector worden
berekend door de procedure f (die 1 argument neemt) uit te voeren
op de originele elementen uit de vector vec.
| (define (vector-map! f v) | | (do ((i 0 (+ i 1))) | | ((= i (vector-length v))) | | (vector-set! v i (f (vector-ref v i))))) |
|
|
|
| > (define v (vector 1 2 3 4)) |
| > (vector-map! (lambda (x) (* x x)) v) |
| > v |
#(1 4 9 16) |
7.2 Vectoren transformeren: vector-map
Schrijf een procedure (vector-map f vec), die een nieuwe vector teruggeeft.
De elementen van de nieuwe vector worden berekend door de procedure f (die 1 argument neemt)
uit te voeren op de overeenkomstige elementen uit de vector vec.
| (define (vector-map f v) | | (let ((result-vector (make-vector (vector-length v)))) | | (do ((i 0 (+ i 1))) | | ((= i (vector-length v)) result-vector) | | (vector-set! result-vector i (f (vector-ref v i)))))) |
|
|
|
| > (vector-map (lambda (x) (* x x)) (vector 1 2 3 4)) |
#(1 4 9 16) |
7.3 Stukken uit een vector selecteren: vector-slice
Schrijf een procedure (vector-slice begin end vect) die een vector teruggeeft
waarvan de elementen overeenkomen met de elementen op de posities begin t.e.m.
end in de input-vector vect.
Je mag ervan uitgaan dat end altijd groter of gelijk aan begin is.
| (define (vector-slice begin end vect) | | (let* ((v-length (+ 1 (- end begin))) | | (v (make-vector v-length))) | | (do ((i 0 (+ i 1))) | | ((= i v-length) v) | | (vector-set! v i (vector-ref vect (+ begin i)))))) |
|
|
|
| > (vector-slice 2 6 (vector 0 1 2 3 4 5 6 7 8 9)) |
#(2 3 4 5 6) |
| > (vector-slice 3 3 (vector 0 1 2 3 4 5 6 7 8 9)) |
#(3) |
| > (vector-slice 4 5 (vector "the" "quick" "brown" "fox" "jumps" "over" "the" "lazy" "dog")) |
#("jumps" "over") |
7.4 Vectoren aaneen plakken: vector-append
Schrijf een procedure vector-append om twee vectoren aaneen te plakken.
| (define (vector-append v1 v2) | | (let ((result-vector (make-vector (+ (vector-length v1) | | (vector-length v2))))) | | (do ((i 0 (+ i 1))) | | ((= i (vector-length v1))) | | (vector-set! result-vector | | i | | (vector-ref v1 i))) | | (do ((i 0 (+ i 1))) | | ((= i (vector-length v2))) | | (vector-set! result-vector | | (+ (vector-length v1) i) | | (vector-ref v2 i))) | | result-vector)) |
|
|
|
| > (vector-append (vector 1 2 3) (vector 4 5 6 7)) |
#(1 2 3 4 5 6 7) |
7.5 Voorspel het resultaat van expressies met destructieve operaties
Gegeven de definities:
| (define x (list '(a b) '(c d))) | | (define y (cons x (cdr x))) |
|
|
|
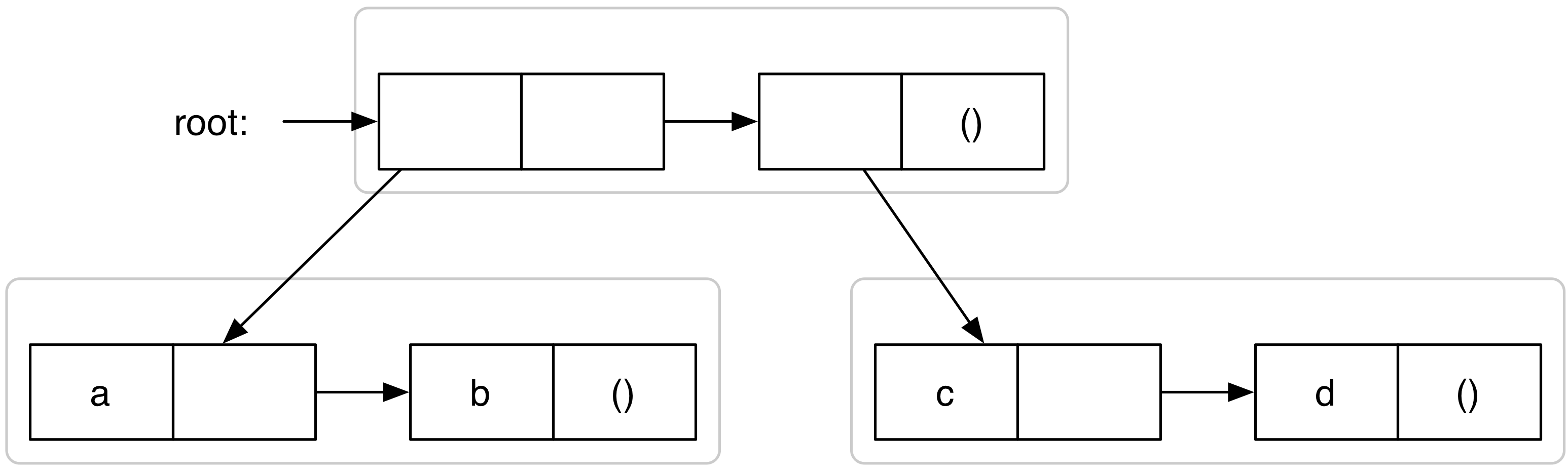
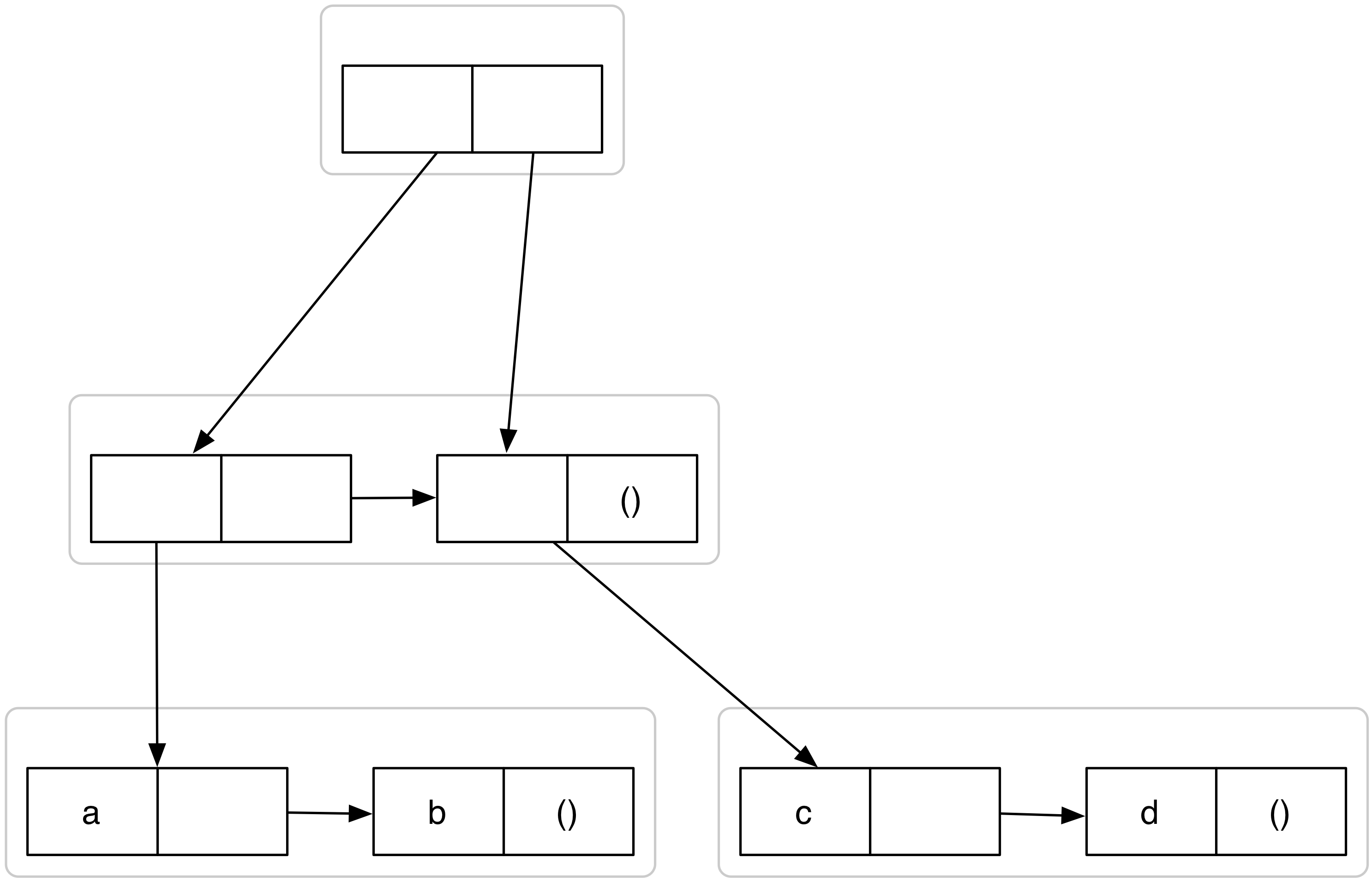
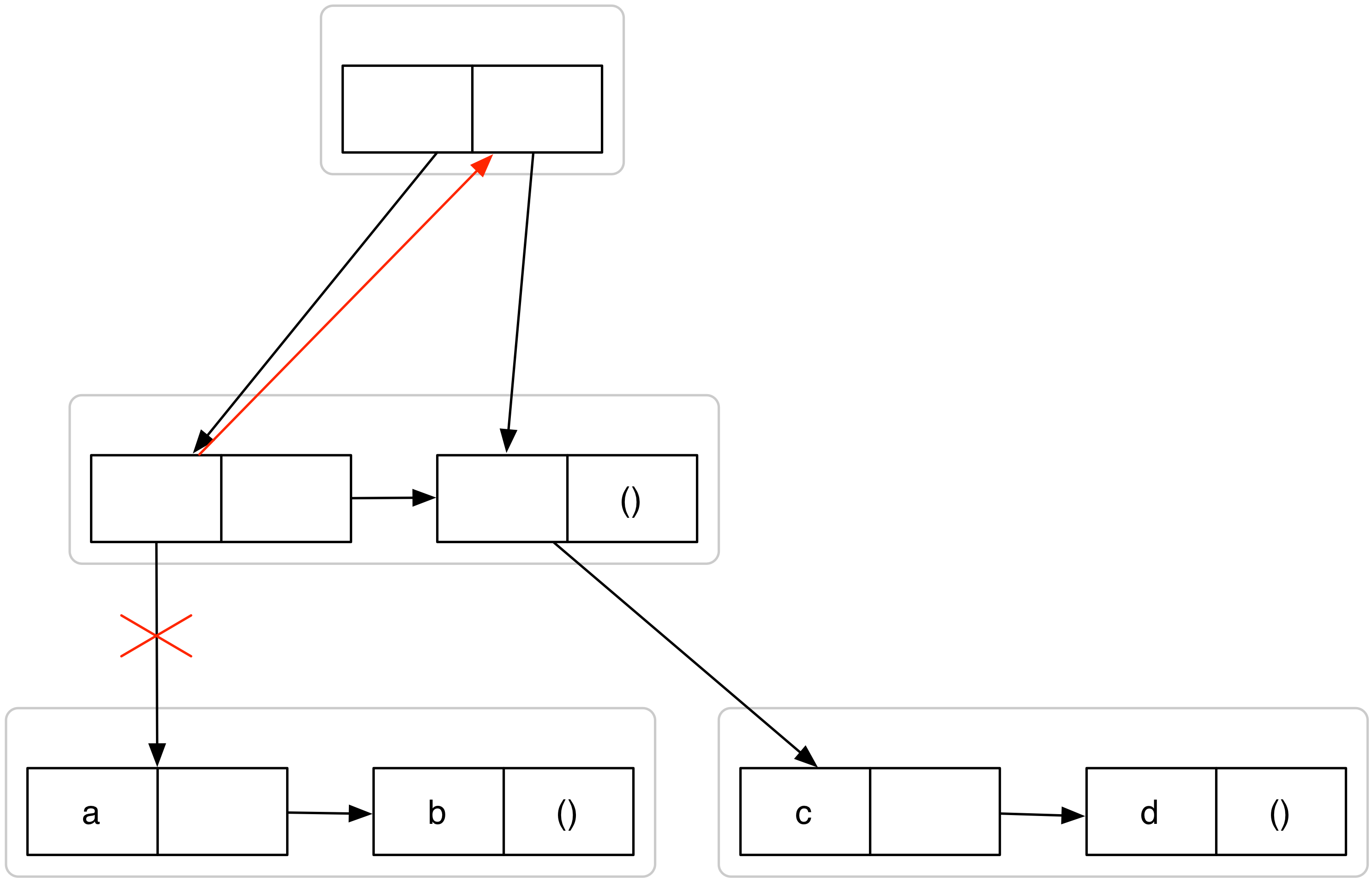
Voorspel dan het resultaat van de evaluatie (in volgorde) van volgende
expressies (teken box-pointer diagrammen):
| > (set-car! (car y) (cdr y)) |
| > y |
((((c d)) (c d)) (c d)) |
7.6 Circulaire Datastructuren: make-ring!
Schrijf een functie (make-ring! n) die een positief geheel
getal neemt en er een ring van maakt (een ring is een circulaire lijst
van n tot 0).
| (define (make-ring! n) | | (let ((last (cons 0 '()))) | | (define (build-list n) | | (if (= n 0) | | last | | (cons n (build-list (- n 1))))) | | (let ((ring (build-list n))) | | (set-cdr! last ring) | | ring))) |
|
|
|
De volgende hulpprocedure is een procedure die er (gelukkig) in slaagt
een constructie met oneindige lussen op eindige manier af te drukken.
| (define (print-ring r) | | (define (aux l) | | (if (not (null? l)) | | (cond ((eq? (cdr l) r) (display " ") | | (display (car l)) | | (display "...")) | | (else (display " ") | | (display (car l)) | | (aux (cdr l)))))) | | (aux r)) |
|
|
|
| > (define r (make-ring! 3)) |
| > (print-ring r) |
3 2 1 0... |
| > (print-ring (cdr r)) |
2 1 0 3... |
7.7 Circulaire Datastructuren: shift-forward
Schrijf een procedure (shift-forward r) die een circulaire lijst 1 plaats voorwaarts verschuift.
| (define (shift-forward r) | | (cdr r)) |
|
|
|
| > (define r (make-ring 3)) |
| > (print-ring (shift-forward r)) |
2 1 0 3... |
7.8 Circulaire Datastructuren: shift-backward
Schrijf een procedure (shift-backward r) die een circulaire lijst 1 plaats achterwaarts verschuift.
| (define (shift-backward r) | | (define (iter l) | | (if (eq? (cdr l) r) | | l | | (iter (cdr l)))) | | (iter r)) |
|
|
|
| > (define r (make-ring 3)) |
| > (print-ring (shift-backward r)) |
0 3 2 1... |
7.9 Destructieve Procedures: map!
Schrijf een destructieve versie van map: (map! f lst) die een bestaande lijst aanpast
(zonder nieuwe cons-cellen aan te maken).
De nieuwe elementen van deze lijst worden berekend door de functie f (die 1 argument neemt)
uit te voeren op de originele elementen uit de lijst lst.
| (define (map! f lst) | | (cond ((not (null? lst)) | | (set-car! lst (f (car lst))) | | (map! f (cdr lst))))) |
|
|
|
| > (define l '(1 2 3 4)) |
| > (map! (lambda (x) (* x x)) l) |
| > l |
(1 4 9 16) |
7.10 Destructieve Procedures: schuif-in!
Een procedure schuif-in! neemt als invoer twee lijsten en transformeert deze twee lijsten in 1 enkele lijst door afwisselend een element van de eerste en van de tweede lijst te nemen.
Schrijf nu een destructieve versie schuif-in! van de procedure.
D.w.z. dat geen enkele nieuwe cons-cel mag aangemaakt worden.
De procedure schuif-in! neemt als invoer de twee gegeven lijsten, en transformeert de eerste ervan op destructieve wijze in het gewenste resultaat.
| (define (schuif-in! l1 l2) | | (cond ((null? (cdr l1)) (set-cdr! l1 l2) 'ok) | | ((null? l2) 'ok) | | (else | | (let ((rest1 (cdr l1)) | | (rest2 (cdr l2))) | | (set-cdr! l1 l2) | | (set-cdr! l2 rest1) | | (schuif-in! rest1 rest2))))) |
|
|
|
| > (define lijst1 '(1 3 5)) |
| > (define lijst2 '(2 4 6 8)) |
| > (schuif-in! lijst1 lijst2) |
ok |
7.11 Destructieve Procedures: merge!
Reisbureau "Happy" en reisbureau "Tours" hebben besloten te fusioneren. Hiertoe
moeten ze hun klantenbestanden samenvoegen. In beide gevallen wordt het
klantenbestand voorgesteld door een geneste lijst, waarin van elke klant naam en
adres wordt bijgehouden en die gesorteerd werd op naam. Bijvoorbeeld:
| (define best1 '((ann (meiboomstraat 12 1820 Eppegem)) | | (bert (populierendreef 7 1050 Brussel)) | | (kurt (Mechelsesteenweg 50 1800 Vilvoorde)))) | | | | (define best2 '((bert (populierendreef 7 1050 Brussel)) | | (jan (eikestraat 1 9000 Gent)) | | (sofie (boerendreef 5 2800 Mechelen)))) |
|
|
|
Deze twee bestanden moeten samengevoegd worden tot een nieuwe gesorteerde
geneste lijst, maar doordat zulke bestanden vrij groot kunnen zijn, moet dit
destructief gebeuren. Bovendien kan het gebeuren dat sommige personen klant
waren bij beide bureaus en dus reeds in de twee bestanden zitten.
7.11.1 Box-pointer diagram
Teken een box-pointer diagram van hoe je het probleem gaat aanpakken op het
gegeven voorbeeld.
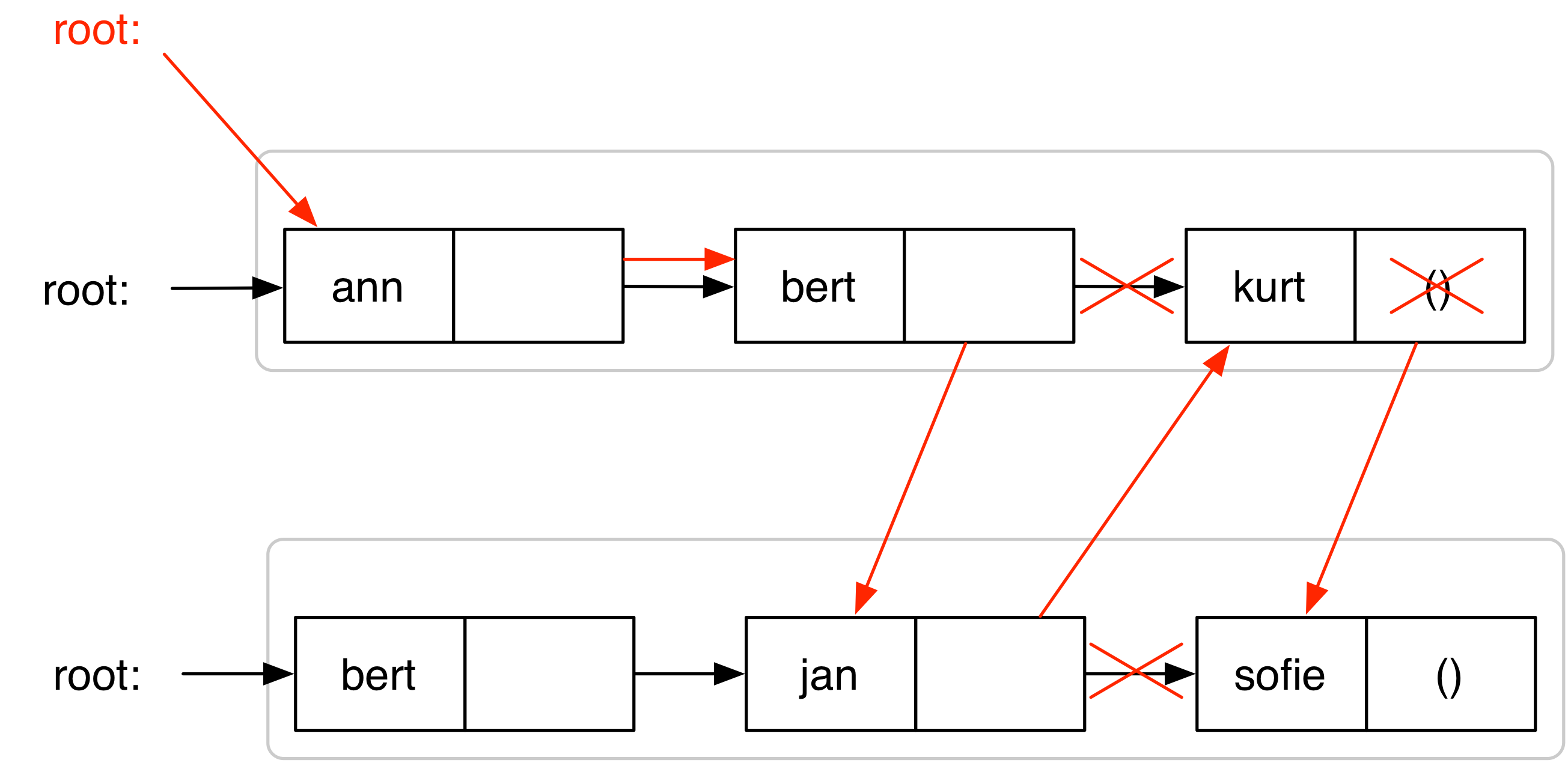
7.11.2 Samenvoegen van klantenbestanden
Schrijf een procedure (merge best1 best2) die de twee bestanden best1
en best2 destructief samenvoegt tot een nieuwe gesorteerde lijst. Hou rekening
met de dubbels.
| (define (symbol<? s1 s2) | | (string<? (symbol->string s1) (symbol->string s2))) | | | | (define (element=? el1 el2) | | (equal? el1 el2)) | | | | (define (merge best1 best2) | | (define (merge-in current rest1 rest2) | | (cond ((null? rest1) (set-cdr! current rest2)) | | ((null? rest2) (set-cdr! current rest1)) | | ((element=? (car rest1) (car rest2)) | | (set-cdr! current rest1) | | (merge-in rest1 (cdr rest1) (cdr rest2))) | | ((symbol<? (caar rest1) (caar rest2)) | | (set-cdr! current rest1) | | (merge-in rest1 (cdr rest1) rest2)) | | (else | | (set-cdr! current rest2) | | (merge-in rest2 rest1 (cdr rest2))))) | | | | (let* ((current (if (symbol<? (caar best1) (caar best2)) | | best1 | | best2)) | | (rest1 (cdr current)) | | (rest2 (if (eq? current best1) best2 best1))) | | (merge-in current rest1 rest2) | | current)) |
|
|
|
| > (merge best1 best2) |
((ann (meiboomstraat 12 1820 Eppegem)) | (bert (populierendreef 7 1050 Brussel)) | (jan (eikestraat 1 9000 Gent)) | (kurt (Mechelsesteenweg 50 1800 Vilvoorde)) | (sofie (boerendreef 5 2800 Mechelen))) |
|
Je kan hiervoor gebruik maken van de volgende hulpprocedures:
| (define (symbol<? s1 s2) | | (string<? (symbol->string s1) (symbol->string s2))) | | | | (define (element=? el1 el2) | | (equal? el1 el2)) |
|
|
|
7.12 Extra Oefeningen
7.12.1 Copy ring
Schrijf een functie copy-ring die een kopie van een circulaire lijst teruggeeft.
| (define (copy-ring r) | | (define last '()) | | (define (aux l) | | (cond ((eq? (cdr l) r) | | (set! last (cons (car l) '())) | | last) | | (else (cons (car l) (aux (cdr l)))))) | | | | (let ((first (aux r))) | | (set-cdr! last first) | | first)) |
|
|
|
| > (define r (make-ring 3)) |
| > (define s (copy-ring r)) |
| > (print-ring s) |
3 2 1 0... |
| > (print-ring s) |
999 2 1 0... |
| > (print-ring r) |
3 2 1 0... |
| > (print-ring s) |
999 888 1 0... |
| > (print-ring r) |
3 2 1 0... |
7.12.2 Het Josephus probleem
Schrijf een functie (josephus r n) die een circulaire lijst
afloopt en telkens het n-de element verwijdert, totdat er
slechts 1 element over is. Dat laatste wordt als resultaat
teruggegeven. Je mag procedures gebruiken die we hierboven
gedefinieerd hebben.
| (define (josephus r n) | | (define (remove-nth! l n) | | (if (<= n 2) | | (begin (set-cdr! l (cddr l)) | | (cdr l)) | | (remove-nth! (cdr l) (- n 1)))) | | | | (define (iter l) | | (print-ring l) | | (if (eq? l (cdr l)) | | (car l) | | (iter (remove-nth! l n)))) | | | | (if (= n 1) | | (car (right-rotate r)) | | (iter (copy-ring r)))) |
|
|
|
| > (define ring (make-ring 5)) |
| > (josephus ring 5) |
5 4 3 2 1 0... 0 5 4 3 2... 0 5 4 3... 5 4 3... 3 5... 5... |
5 |
| > (print-ring ring) |
5 4 3 2 1 0... |
7.12.3 Neveneffecten bij append
Als je weet dat append in Scheme gedefinieerd is zoals hieronder, en met de volgende definities voor l1, l2 en l3:
| (define (append x y) |
| (cond ((null? x) y) |
| (else (cons (car x) |
| (append (cdr x) y))))) |
| (define l1 '(1 2 3)) | | (define l2 '(4 5)) | | (define l3 (append l1 l2)) |
|
|
|
Voorspel dan de waarden van l1, l2 en l3 na evaluatie van elk van de volgende expressies:
| > (set-car! (cdddr l3) 9) |
7.12.4 Examen Wiskunde 1ste zit 1994
Schrijf een destructieve procedure (kw-lijst lst) die een circulaire lijst
omvormt tot een circulaire lijst met twee keer zoveel elementen, door
vlak na ieder element van de lijst een nieuw element tussen te voegen
waarvan de waarde gelijk is aan het kwadraat van het oorspronkelijke
element. Bijvoorbeeld, de lijst met box-pointer diagram
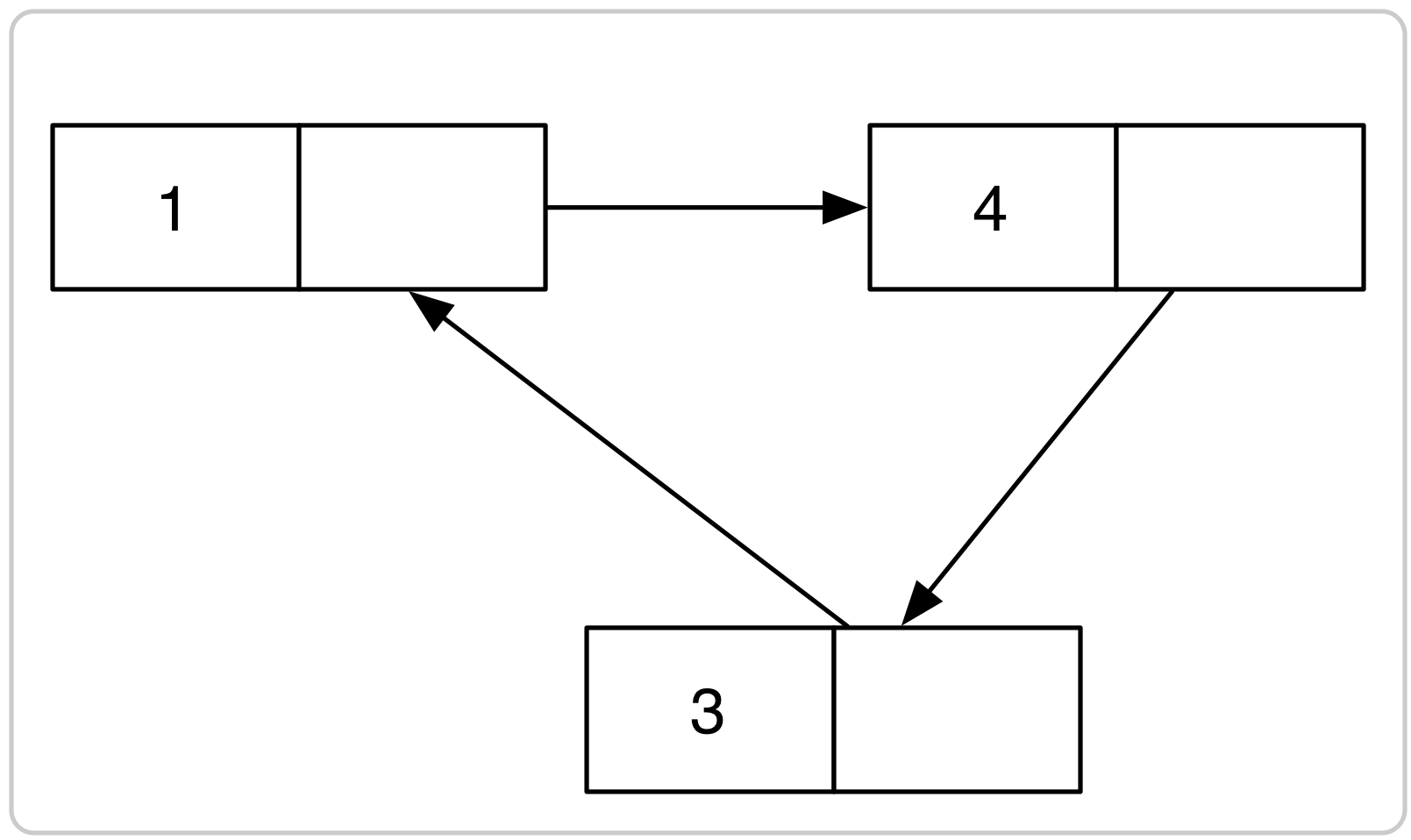
wordt omgevormd tot de volgende circulaire lijst:
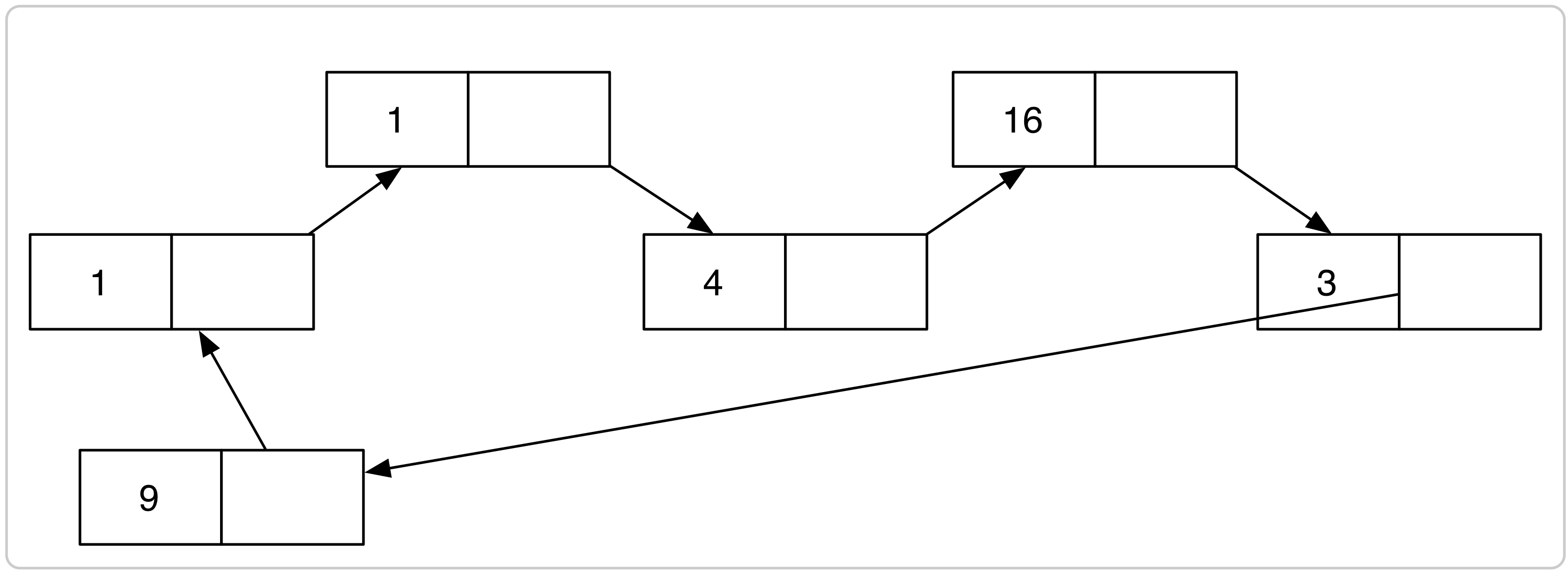
| (define (kw-lijst lst) | | (define (loop l) | | (let ((rest (cdr l)) | | (n (list (* (car l) (car l))))) | | (set-cdr! l n) | | (set-cdr! n rest) | | (if (not (eq? rest lst)) | | (loop rest)))) | | (loop lst) | | lst) |
|
|
|
| > (define last-cons (cons 3 '())) |
| > (define test-lst (cons 1 (cons 4 last-cons))) |
| > (set-cdr! last-cons test-lst) |
| > (print-ring (kw-lijst test-lst)) |
1 1 4 16 3 9... |
7.12.5 Examen Informatica 1ste zit 1996
Schrijf een destructieve procedure ontdubbel! die een (platte) lijst van getallen als invoer neemt, en een cons-cel teruggeeft met als car de lijst van alle even elementen van de oorspronkelijke lijst, en als cdr de lijst van alle oneven elementen van de oorspronkelijke lijst. Bovendien is dit de enige(!) nieuwe cons-cel die je procedure mag aanmaken. Let ook op dat de onderliggende volgorde der elementen behouden blijft.
| (define (ontdubbel! lijst) | | (let ((deEven '()) | | (deOneven '())) | | (define (ontdubbel-iter prevE prevO restLijst) | | (cond ((null? restLijst) (set-cdr! prevE '()) | | (set-cdr! prevO '()) | | (cons deEven deOneven)) | | ((even? (car restLijst)) | | (if (null? prevE) | | (set! deEven restLijst) | | (set-cdr! prevE restLijst)) | | (ontdubbel-iter restLijst prevO (cdr restLijst))) | | (else (if (null? prevO) | | (set! deOneven restLijst) | | (set-cdr! prevO restLijst)) | | (ontdubbel-iter prevE restLijst (cdr restLijst))))) | | (ontdubbel-iter deEven deOneven lijst))) |
|
|
|
| > (ontdubbel! '(1 2 3 4 5 6 7 8 9 10)) |
((2 4 6 8 10) 1 3 5 7 9) |
7.12.6 Examen januari 2004: Destructief
Schrijf destrucief een functie (insert! lst1 lst2) die twee lijsten lst1 en lst2 als parameter neemt.
De lijst lst1 is een lijst van (niet lege!) lijstjes, de lijst lst2 is een lijst met symbolen.
De functie insert! voegt de symbolen van lst2 toe aan de achterkant van de lijstjes in lst1.
Hou er rekening mee dat je geen enkele nieuwe cons-cel mag aanmaken! Je mag alleen maar bestaande cons-cellen wijzigen.
Je mag ervan uitgaan dat de lijstjes lst1 en lst2 even lang zijn.
| (define (insert-aux! lst lst2) | | (set-cdr! lst2 '()) | | (if (null? (cdr lst)) | | (set-cdr! lst lst2) | | (insert-aux! (cdr lst) lst2)) | | lst) | | | | (define (insert! lst1 lst2) | | (if (not (null? lst1)) | | (begin | | (insert! (cdr lst1) (cdr lst2)) | | (insert-aux! (car lst1) lst2) | | lst1))) |
|
|
|
| > (insert-aux! '(a 12 q) '(v w x y z)) |
(a 12 q v) |
| > (insert! '((a 12 q) (b 13) (c 14 r s) (f 18) (j 22 t)) '(v w x y z)) |
((a 12 q v) (b 13 w) (c 14 r s x) (f 18 y) (j 22 t z)) |
7.12.7 Examen januari 2008: Destructief
Schrijf een destructieve procedure all-but-interval die een stijgend
geordende lijst van getallen neemt en alle getallen in een gegeven interval
verwijdert. Er worden twee parameters doorgegeven om het interval aan te
duiden, en de eerste is kleiner of gelijk aan de tweede.
| (define (all-but-interval lst min max) | | (define (aux last-smaller-cons aux-lst) | | (cond | | ((null? aux-lst) | | (set-cdr! last-smaller-cons '())) | | ((< (car aux-lst) min) | | (aux aux-lst (cdr aux-lst))) | | ((> (car aux-lst) max) | | (set-cdr! last-smaller-cons aux-lst)) | | (else | | (aux last-smaller-cons (cdr aux-lst))))) | | (aux lst lst) | | lst) |
|
|
|
| > (all-but-interval '(1 2 3 4 5 6) 2 4) |
(1 5 6) |
| > (all-but-interval '(1 2 3 4 5) 2 2) |
(1 3 4 5) |
| > (all-but-interval '(1 2 5 6 7) 3 9) |
(1 2) |